题目内容
3. 如图,D,E分别是△ABC边AB,BC上的点,AD=2BD,BE=CE,若S△ABC=30,则四边形BEFD的面积为( )
如图,D,E分别是△ABC边AB,BC上的点,AD=2BD,BE=CE,若S△ABC=30,则四边形BEFD的面积为( )| A. | 5 | B. | 7 | C. | 9 | D. | 10 |
分析 作DM∥AE,交BC于M,根据平行线分线段成比例定理求得三角形ADF的面积,进而根据已知条件求得三角形ABE的面积,根据S四边形BDFE=S△ABE-S△ADF即可求得.
解答 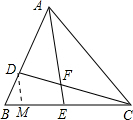 解:作DM∥AE,交BC于M,
解:作DM∥AE,交BC于M,
∴$\frac{AD}{BD}$=$\frac{EM}{BM}$,
∵AD=2BD,
∴$\frac{EM}{BM}$=$\frac{2}{1}$,
∴EM=$\frac{2}{3}$BE,
∴BE=CE,
∴$\frac{EC}{EM}$=$\frac{3}{2}$,
∵DM∥AE,
∴$\frac{CF}{DF}$=$\frac{EC}{EM}$=$\frac{3}{2}$,
∴$\frac{CF}{CD}$=$\frac{3}{5}$,
∴$\frac{DF}{CD}=\frac{2}{5}$
∴$\frac{{S}_{△ADF}}{{S}_{△ACD}}=\frac{2}{5}$,
∵AD=2BD,
∴S△ADC=$\frac{2}{3}$S△ABC=$\frac{2}{3}$×30=20,
∴S△ADF=$\frac{2}{5}$×20=8,
∵S△ABE=S△ACE=$\frac{1}{2}$S△ABC=15,
∴S四边形BDFE=S△ABE-S△ADF=15-8=7.
故选B.
点评 本题考查三角形的面积,关键知道当高相等时,面积等于底边的比,底相等时,面积等于高的比,根据此可求出三角形的面积,然后求出差.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.若a+b=-1,则a2+b2+2ab的值为( )
| A. | 1 | B. | -1 | C. | 3 | D. | -3 |
15.若a、b、c都不为0,化简$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$+$\frac{{|{abc}|}}{abc}$结果有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
12.二次函数y=2x2+x-1的图象与x轴的交点的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
13.若A(-2,y1),B(-1,y2),C(-3,y3)为二次函数y=ax2(a<0)的图象上的三点,则y1,y2,y3的大小关系是( )
| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y3<y1<y2 | D. | y1<y3<y2 |
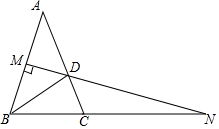 如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线MN交BC的延长线于点N,交AC于点D,连接BD,AD=6,
如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线MN交BC的延长线于点N,交AC于点D,连接BD,AD=6,