题目内容
12.二次函数y=2x2+x-1的图象与x轴的交点的个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 求出判别式的值,根据抛物线与x轴的交点个数的判定方法判断即可.
解答 解:△=12-4×2×(-1)=9>0,
则二次函数y=2x2+x-1的图象与x轴的交点的个数是2,
故选:C.
点评 本题考查的是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0根之间的关系,△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
20.正数x的算术平方根是( )
| A. | x | B. | $\sqrt{x}$ | C. | ±$\sqrt{x}$ | D. | |x| |
7.下列四边形中,一定有外接圆的是( )
| A. | 平行四边形 | B. | 菱形 | C. | 矩形 | D. | 任意四边形 |
17.将△ABC的各边都扩大3倍,则∠A的三个三角函数值都( )
| A. | 扩大3倍 | B. | 缩小3倍 | C. | 不变 | D. | 无法确定 |
2.下列运算正确的是( )
| A. | $\sqrt{6}$+$\sqrt{3}$=3 | B. | 3$\sqrt{2}$-$\sqrt{2}$=3 | C. | $\sqrt{2}$×$\sqrt{8}$=4 | D. | $\sqrt{6}$÷$\sqrt{3}$=2 |
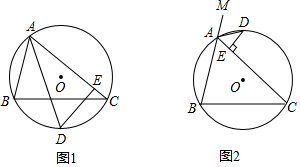
 如图,D,E分别是△ABC边AB,BC上的点,AD=2BD,BE=CE,若S△ABC=30,则四边形BEFD的面积为( )
如图,D,E分别是△ABC边AB,BC上的点,AD=2BD,BE=CE,若S△ABC=30,则四边形BEFD的面积为( )