题目内容
15.若a、b、c都不为0,化简$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$+$\frac{{|{abc}|}}{abc}$结果有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 直接利用a,b,c中符号不同所得结果有可能不同进而分析得出答案.
解答 解:当a,b,c中有一正两负,
则$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$+$\frac{{|{abc}|}}{abc}$=0,
当a,b,c中有2正1负,
则$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$+$\frac{{|{abc}|}}{abc}$=0,
当a,b,c中有3正,
则$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$+$\frac{{|{abc}|}}{abc}$=4,
当a,b,c中有3负,
则$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$+$\frac{{|{abc}|}}{abc}$=-4,
故其结果共有3个.
故选:B.
点评 此题主要考查了绝对值,正确把握相关性质是解题关键.

练习册系列答案
相关题目
18.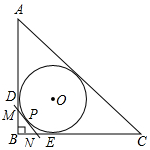 如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D、E,过劣弧(不包括端点D、E)上任一点P作⊙O的切线MN与AB、BC分别交于点M、N,若⊙O的半径为r.
如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D、E,过劣弧(不包括端点D、E)上任一点P作⊙O的切线MN与AB、BC分别交于点M、N,若⊙O的半径为r.
求:Rt△MBN的周长.
 如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D、E,过劣弧(不包括端点D、E)上任一点P作⊙O的切线MN与AB、BC分别交于点M、N,若⊙O的半径为r.
如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D、E,过劣弧(不包括端点D、E)上任一点P作⊙O的切线MN与AB、BC分别交于点M、N,若⊙O的半径为r.求:Rt△MBN的周长.
20.正数x的算术平方根是( )
| A. | x | B. | $\sqrt{x}$ | C. | ±$\sqrt{x}$ | D. | |x| |
7.下列四边形中,一定有外接圆的是( )
| A. | 平行四边形 | B. | 菱形 | C. | 矩形 | D. | 任意四边形 |
5.如图,用长度相等的小木棒搭成的三角形网格,根据图示填写下列表格.
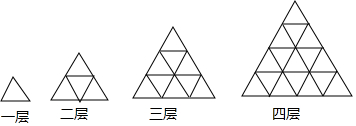

| 层数 | 1 | 2 | 3 | 4 | … | n |
| 所含小三角形的个数 | 1 | 4 | 9 | 16 | … | 4n-3 |
| 所需小木棒的根数 | 3 | 9 | 18 | 30 | … | $\frac{3}{2}$n(n+1) |
 如图,线段AB绕点0O转后,点A旋转到点A′,画出线段AB绕点O转后所得的迭段.
如图,线段AB绕点0O转后,点A旋转到点A′,画出线段AB绕点O转后所得的迭段. 如图,D,E分别是△ABC边AB,BC上的点,AD=2BD,BE=CE,若S△ABC=30,则四边形BEFD的面积为( )
如图,D,E分别是△ABC边AB,BC上的点,AD=2BD,BE=CE,若S△ABC=30,则四边形BEFD的面积为( )