题目内容
11.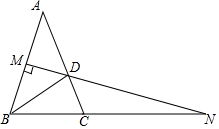 如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线MN交BC的延长线于点N,交AC于点D,连接BD,AD=6,
如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线MN交BC的延长线于点N,交AC于点D,连接BD,AD=6,(1)求∠N的度数;
(2)求BC的长.
分析 (1)根据等腰三角形的性质和三角形内角和定理可求∠ABC的度数,再根据直角三角形的性质可求∠N的度数;
(2)根据线段垂直平分线的性质可求BD=AD,根据等腰三角形的判定和性质可求BC的长.
解答 解:(1)∵在△ABC中,AB=AC,∠A=36°,
∴∠ABC=∠ACB=(180°-36°)÷2=72°,
∵MN⊥AB,
∴∠BMN=90°,
∴∠N=90°-72°=18°;
(2)∵AB的垂直平分线MN交BC的延长线于点N,
∴∠ABD=∠A=36°,BD=AD=6,
∴∠BDC=72°,
∴∠BDC=∠ACB,
∴BC=BD=6.
点评 本题考查的是等腰三角形的性质,线段垂直平分线的性质,熟知垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
相关题目
2.下列不是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{x+y=3}\\{x-y=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+\frac{1}{y}=0}\\{y+x=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{6x+4y=9}\\{y=3x+4}\end{array}\right.$ |
7.下列四边形中,一定有外接圆的是( )
| A. | 平行四边形 | B. | 菱形 | C. | 矩形 | D. | 任意四边形 |
 如图,线段AB绕点0O转后,点A旋转到点A′,画出线段AB绕点O转后所得的迭段.
如图,线段AB绕点0O转后,点A旋转到点A′,画出线段AB绕点O转后所得的迭段.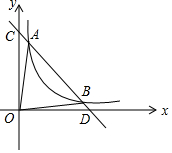 如图,已知一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A(1,6),B(3,n)两点.
如图,已知一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A(1,6),B(3,n)两点. 如图,D,E分别是△ABC边AB,BC上的点,AD=2BD,BE=CE,若S△ABC=30,则四边形BEFD的面积为( )
如图,D,E分别是△ABC边AB,BC上的点,AD=2BD,BE=CE,若S△ABC=30,则四边形BEFD的面积为( )