题目内容
3.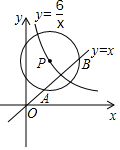 如图,已知在平面直角坐标系xOy中,O为坐标原点,点P是反比例函数y=$\frac{6}{x}$(x>0)图象上的一个动点,若以点P为圆心,3为半径的圆与直线y=x相交,交点为A、B,当弦AB的长等于2$\sqrt{5}$时,点P的坐标为( )
如图,已知在平面直角坐标系xOy中,O为坐标原点,点P是反比例函数y=$\frac{6}{x}$(x>0)图象上的一个动点,若以点P为圆心,3为半径的圆与直线y=x相交,交点为A、B,当弦AB的长等于2$\sqrt{5}$时,点P的坐标为( )| A. | (1,6)和(6,1) | B. | (2,3)和(3,2) | C. | ($\sqrt{2}$,3$\sqrt{2}$)和(3$\sqrt{2}$,$\sqrt{2}$) | D. | ($\sqrt{3}$,2$\sqrt{3}$)和(2$\sqrt{3}$,$\sqrt{3}$) |
分析 当点P在直线y=x上方时,作PH⊥AB,利用垂径定理可得AH=$\sqrt{5}$,由勾股定理易得PH,作PM⊥x轴交直线AB于点C,由PH可得CP,设OM=a,则CM=a,易得,P(a,a$+2\sqrt{2}$),因为P点在反比例函数图象上,所以易得a(a$+2\sqrt{2}$)=6,可得a,易得P点的坐标,当点P在直线y=x下方时,利用对称性可得P点的另一坐标.
解答 解:当点P在直线y=x上方时,连接PA,作PH⊥AB,
∴AH=$\sqrt{5}$,而PA=3
∴PH=2.
作PM⊥x轴交直线AB于点C,
设OM=a,则CM=a,而PC=2$\sqrt{2}$,∴P(a,a$+2\sqrt{2}$),
∴a(a$+2\sqrt{2}$)=6,
∴a=$\sqrt{2}$,
∴P($\sqrt{2}$,3$\sqrt{2}$),
当点P在直线y=x下方时,由对称性可知P(3$\sqrt{2}$,$\sqrt{2}$),
故选C.
点评 本题主要考查了垂径定理,反比例函数与一次函数的交点,作出恰当的辅助线,利用勾股定理和垂径定理解得PC是解答此题的关键.

练习册系列答案
相关题目
13. 已知S△ABC=4cm2,点E为BC中点,点D为BE中点,则S△ABD=( )cm2.
已知S△ABC=4cm2,点E为BC中点,点D为BE中点,则S△ABD=( )cm2.
 已知S△ABC=4cm2,点E为BC中点,点D为BE中点,则S△ABD=( )cm2.
已知S△ABC=4cm2,点E为BC中点,点D为BE中点,则S△ABD=( )cm2.| A. | 2 | B. | 3 | C. | 1 | D. | 1.5 |
14. 如图,DE为△ABC的边BC的垂直平分线,交BC于E,交AB于D,且∠B=40°,∠A=60°,则∠ACD的度数为( )
如图,DE为△ABC的边BC的垂直平分线,交BC于E,交AB于D,且∠B=40°,∠A=60°,则∠ACD的度数为( )
 如图,DE为△ABC的边BC的垂直平分线,交BC于E,交AB于D,且∠B=40°,∠A=60°,则∠ACD的度数为( )
如图,DE为△ABC的边BC的垂直平分线,交BC于E,交AB于D,且∠B=40°,∠A=60°,则∠ACD的度数为( )| A. | 40° | B. | 50° | C. | 30° | D. | 45° |
11.下列计算正确的是( )
| A. | 0-4=4 | B. | -9-4=-13 | C. | -22=4 | D. | (-3)×0=-3 |
18.下列事件中,属于必然事件的是( )
| A. | 掷一枚硬币,正面朝下 | |
| B. | 三角形两边之和大于第三边 | |
| C. | 一个三角形三个内角的和小于180° | |
| D. | 在一个没有红球的盒子里,摸到红球 |
8.若二次函数y=ax2+c的图象经过点P(1,3),则该图象必经过点( )
| A. | (1,-3) | B. | (-1,3) | C. | (3,-1) | D. | (-3,1) |
 如图,已知∠AOB=45°,P位∠AOB内任一点,且OP=5,若点P关于OA,OB的对称点为P1,P2,连接P1O,P2O,P1P2,求△OP1P2的面积.
如图,已知∠AOB=45°,P位∠AOB内任一点,且OP=5,若点P关于OA,OB的对称点为P1,P2,连接P1O,P2O,P1P2,求△OP1P2的面积.