题目内容
13．
已知S△ABC=4cm2，点E为BC中点，点D为BE中点，则S△ABD=（ ）cm2．| A． | 2 | B． | 3 | C． | 1 | D． | 1.5 |
分析 根据三角形的中线将三角形分成面积相等的两部分解得即可．
解答 解：∵点E为BC中点，点D为BE中点，
∴BD=$\frac{1}{4}$BC，
∴S△ABD=$\frac{1}{4}$S△ABC=14cm2．
故选C．
点评 本题主要考查了三角形面积及三角形面积的等积变换，三角形的中线将三角形分成面积相等的两部分．
练习册系列答案
相关题目
4．以下可以用作证明命题“若a＞b，则|a|＞|b|”是假命题的反例的是（ ）
| A． | a=3，b=2 | B． | a=0，b=-1 | C． | a=2，b=-1 | D． | a=5，b=0 |
1．
已知：如图所示，E为正方形ABCD外一点，AE=AD，∠ADE=75°，则∠AEB=（ ）
已知：如图所示，E为正方形ABCD外一点，AE=AD，∠ADE=75°，则∠AEB=（ ）| A． | 60° | B． | 45° | C． | 30° | D． | 55° |
8．下列说法正确的是（ ）
| A． | $\sqrt{9}$的平方根是±3 | B． | 8的立方根是±2 | C． | 4的平方根是2 | D． | -$\sqrt{2}$是2的平方根 |
已知，如图，AB是⊙O的直径，∠BCD=45°．求证：AD=BD．
5．抛物线y=x2-4与y轴的交点坐标是（ ）
| A． | （0，-4） | B． | （-4，0） | C． | （2，0） | D． | （0，2） |
3．
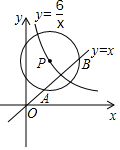如图，已知在平面直角坐标系xOy中，O为坐标原点，点P是反比例函数y=$\frac{6}{x}$（x＞0）图象上的一个动点，若以点P为圆心，3为半径的圆与直线y=x相交，交点为A、B，当弦AB的长等于2$\sqrt{5}$时，点P的坐标为（ ）
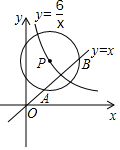如图，已知在平面直角坐标系xOy中，O为坐标原点，点P是反比例函数y=$\frac{6}{x}$（x＞0）图象上的一个动点，若以点P为圆心，3为半径的圆与直线y=x相交，交点为A、B，当弦AB的长等于2$\sqrt{5}$时，点P的坐标为（ ）| A． | （1，6）和（6，1） | B． | （2，3）和（3，2） | C． | （$\sqrt{2}$，3$\sqrt{2}$）和（3$\sqrt{2}$，$\sqrt{2}$） | D． | （$\sqrt{3}$，2$\sqrt{3}$）和（2$\sqrt{3}$，$\sqrt{3}$） |