题目内容
14．
如图，DE为△ABC的边BC的垂直平分线，交BC于E，交AB于D，且∠B=40°，∠A=60°，则∠ACD的度数为（ ）| A． | 40° | B． | 50° | C． | 30° | D． | 45° |
分析 先根据三角形内角和定理求出∠ACB的度数，再由线段垂直平分线的性质求出∠BCD的度数，根据∠ACD=∠ACB-∠BCD即可得出结论．
解答 解：∵∠B=40°，∠A=60°，
∴∠ACB=180°-60°-40°=80°，
∵DE为△ABC边BC的垂直平分线，
∴∠BCD=∠B=40°，
∴∠ACD=∠ACB-∠BCD=80°-40°=40°．
故选A．
点评 本题考查的是线段垂直平分线的性质，熟知垂直平分线上任意一点，到线段两端点的距离相等是解答此题的关键．
练习册系列答案
相关题目
4．以下可以用作证明命题“若a＞b，则|a|＞|b|”是假命题的反例的是（ ）
| A． | a=3，b=2 | B． | a=0，b=-1 | C． | a=2，b=-1 | D． | a=5，b=0 |
5．抛物线y=x2-4与y轴的交点坐标是（ ）
| A． | （0，-4） | B． | （-4，0） | C． | （2，0） | D． | （0，2） |
3．
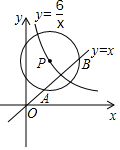如图，已知在平面直角坐标系xOy中，O为坐标原点，点P是反比例函数y=$\frac{6}{x}$（x＞0）图象上的一个动点，若以点P为圆心，3为半径的圆与直线y=x相交，交点为A、B，当弦AB的长等于2$\sqrt{5}$时，点P的坐标为（ ）
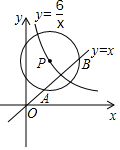如图，已知在平面直角坐标系xOy中，O为坐标原点，点P是反比例函数y=$\frac{6}{x}$（x＞0）图象上的一个动点，若以点P为圆心，3为半径的圆与直线y=x相交，交点为A、B，当弦AB的长等于2$\sqrt{5}$时，点P的坐标为（ ）| A． | （1，6）和（6，1） | B． | （2，3）和（3，2） | C． | （$\sqrt{2}$，3$\sqrt{2}$）和（3$\sqrt{2}$，$\sqrt{2}$） | D． | （$\sqrt{3}$，2$\sqrt{3}$）和（2$\sqrt{3}$，$\sqrt{3}$） |
如图所示，在△ABC中，∠BAC=120°，以BC为边向外作等边三角形BCD，把△ABD绕点D按顺时针方向旋转60°后到△ECD的位置，若AB=6，AC=4，求∠BAD的度数和AD的长．