题目内容
13.通过配方,把下列函数化为y=a(x-h)2+k的形式,并指出函数的最大(或最小)值.(1)y=-2x2-5x+9;(2)y=2x2+3x;
(3)y=$\frac{5}{2}$x2-4x+1;(4)y=-$\frac{3}{4}$x2+$\frac{9}{2}$x-2.
分析 利用配方法先提出二次项系数,再加上一次项系数的一半的平方来凑完全平方式,即可把一般式转化为顶点式,然后根据二次函数的性质求出抛物线的最值.
解答 解:(1)y=-2x2-5x+9
y=-2(x2+$\frac{5}{2}$x)+9
y=-2(x2+$\frac{5}{2}$x+$\frac{25}{16}$-$\frac{25}{16}$)+9
y=-2(x+$\frac{5}{4}$)2+$\frac{25}{8}$+9
y=-2(x+$\frac{5}{4}$)2+$\frac{97}{8}$;
∵a=-2<0,
∴函数有最大值$\frac{97}{8}$;
(2)y=2x2+3x;
y=2(x2+$\frac{3}{2}$x)
y=2(x2+$\frac{3}{2}$x+$\frac{9}{16}$-$\frac{9}{16}$)
y=2(x+$\frac{3}{4}$)2-$\frac{9}{8}$;
∵a=2>0,
∴函数有最小值-$\frac{9}{8}$;
(3)y=$\frac{5}{2}$x2-4x+1;
y=$\frac{5}{2}$(x2-$\frac{8}{5}$x)+1
y=$\frac{5}{2}$(x2-$\frac{8}{5}$x+$\frac{16}{25}$-$\frac{16}{25}$)+1
y=$\frac{5}{2}$(x-$\frac{4}{5}$)2-$\frac{3}{5}$;
∵a=$\frac{5}{2}$>0,
∴函数有最小值-$\frac{3}{5}$;
(4)y=-$\frac{3}{4}$x2+$\frac{9}{2}$x-2,
y=-$\frac{3}{4}$(x2-6x+9-9)-2
y=-$\frac{3}{4}$(x-3)2+$\frac{27}{4}$-2
y=-$\frac{3}{4}$(x-3)2+$\frac{19}{4}$;
∵a=-$\frac{3}{4}$<0,
∴函数有最大值$\frac{19}{4}$.
点评 本题考查了二次函数的性质及二次函数的解析式有三种形式:(1)一般式:y=ax2+bx+c(a≠0,a、b、c为常数);(2)顶点式:y=a(x-h)2+k;(3)交点式(与x轴):y=a(x-x1)(x-x2).

 中考解读考点精练系列答案
中考解读考点精练系列答案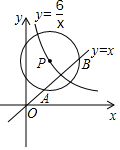 如图,已知在平面直角坐标系xOy中,O为坐标原点,点P是反比例函数y=$\frac{6}{x}$(x>0)图象上的一个动点,若以点P为圆心,3为半径的圆与直线y=x相交,交点为A、B,当弦AB的长等于2$\sqrt{5}$时,点P的坐标为( )
如图,已知在平面直角坐标系xOy中,O为坐标原点,点P是反比例函数y=$\frac{6}{x}$(x>0)图象上的一个动点,若以点P为圆心,3为半径的圆与直线y=x相交,交点为A、B,当弦AB的长等于2$\sqrt{5}$时,点P的坐标为( )| A. | (1,6)和(6,1) | B. | (2,3)和(3,2) | C. | ($\sqrt{2}$,3$\sqrt{2}$)和(3$\sqrt{2}$,$\sqrt{2}$) | D. | ($\sqrt{3}$,2$\sqrt{3}$)和(2$\sqrt{3}$,$\sqrt{3}$) |
 如图,数轴上A,B两点分别对应数a、b,则下列结论不正确的是( )
如图,数轴上A,B两点分别对应数a、b,则下列结论不正确的是( )| A. | |a|>|b| | B. | a+b>0 | C. | ab<0 | D. | |b|=b |
 如图所示,在△ABC中,∠BAC=120°,以BC为边向外作等边三角形BCD,把△ABD绕点D按顺时针方向旋转60°后到△ECD的位置,若AB=6,AC=4,求∠BAD的度数和AD的长.
如图所示,在△ABC中,∠BAC=120°,以BC为边向外作等边三角形BCD,把△ABD绕点D按顺时针方向旋转60°后到△ECD的位置,若AB=6,AC=4,求∠BAD的度数和AD的长. 如图,在△ABC中,点D、E分别是AC、AB上的点,AC=7,∠EDC=60°,∠ABC=120°,AE=BC,sinA=$\frac{3\sqrt{3}}{14}$,则四边形DEBC的面积为$\frac{150\sqrt{3}}{49}$.
如图,在△ABC中,点D、E分别是AC、AB上的点,AC=7,∠EDC=60°,∠ABC=120°,AE=BC,sinA=$\frac{3\sqrt{3}}{14}$,则四边形DEBC的面积为$\frac{150\sqrt{3}}{49}$.