题目内容
 在△ABC中,∠BAC=90°,AB=AC,∠ABC=∠ACB=45°,如图所示,点D、E分别是AB、AC边的中点,AF⊥BE交BC于点F,连结EF、CD交于点H.
在△ABC中,∠BAC=90°,AB=AC,∠ABC=∠ACB=45°,如图所示,点D、E分别是AB、AC边的中点,AF⊥BE交BC于点F,连结EF、CD交于点H.(1)求证:△ABE≌△ACD;
(2)求证:∠EAF=∠ACD;
(3)猜想直线EF与直线CD的位置关系.
考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)易证AD=AE,即可证明△ABE≌△ACD;
(2)易证∠EAF=∠ABE,根据(1)中结论可得∠ABE=∠ACD,即可解题;
(3)过点C作CM⊥AC交AF延长线于点M,易证△ABE≌△CAM,可得AE=CM,∠AEB=∠M,即可证明△EFC≌△MCF,可得∠FEC=∠M,即可证明△ABE≌△ACD,可得∠ABE=∠ACD,即可解题.
(2)易证∠EAF=∠ABE,根据(1)中结论可得∠ABE=∠ACD,即可解题;
(3)过点C作CM⊥AC交AF延长线于点M,易证△ABE≌△CAM,可得AE=CM,∠AEB=∠M,即可证明△EFC≌△MCF,可得∠FEC=∠M,即可证明△ABE≌△ACD,可得∠ABE=∠ACD,即可解题.
解答:解:(1)∵点D、E分别是AB、AC边的中点,∴AD=AE,
∵在△ABE和△ACD中,
,
∴△ABE≌△ACD,(SAS);
(2)∵∠EAF+∠AEB=90°,∠ABE+∠AEB=90°,
∴∠EAF=∠ABE,
∵△ABE≌△ACD,
∴∠ABE=∠ACD,
∴∠EAF=∠ACD;
(3)证明:如图,过点C作CM⊥AC交AF延长线于点M,

∵在△ABE和△CAM中,
,
∴△ABE≌△CAM(ASA),
∴AE=CM,∠AEB=∠M,
∵AE=EC,
∴EC=CM,
∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∵∠ACM=90°,
∴∠FCM=90-45°=45°=∠ACF,
在△EFC和△MFC中,
,
∴△EFC≌△MCF(SAS),
∴∠FEC=∠M,
∴∠FEC=∠FCM,
∵AB=AC,点D、E分别是AB、AC边的中点,
∴AD=AE,
在△ABE与△ACD中,
,
∴△ABE≌△ACD(SAS)
∴∠ABE=∠ACD,
∴∠ACD+∠FEC=90°,
∴∠EHC=90°,
∴EF⊥CD.
∵在△ABE和△ACD中,
|
∴△ABE≌△ACD,(SAS);
(2)∵∠EAF+∠AEB=90°,∠ABE+∠AEB=90°,
∴∠EAF=∠ABE,
∵△ABE≌△ACD,
∴∠ABE=∠ACD,
∴∠EAF=∠ACD;
(3)证明:如图,过点C作CM⊥AC交AF延长线于点M,

∵在△ABE和△CAM中,
|
∴△ABE≌△CAM(ASA),
∴AE=CM,∠AEB=∠M,
∵AE=EC,
∴EC=CM,
∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∵∠ACM=90°,
∴∠FCM=90-45°=45°=∠ACF,
在△EFC和△MFC中,
|
∴△EFC≌△MCF(SAS),
∴∠FEC=∠M,
∴∠FEC=∠FCM,
∵AB=AC,点D、E分别是AB、AC边的中点,
∴AD=AE,
在△ABE与△ACD中,
|
∴△ABE≌△ACD(SAS)
∴∠ABE=∠ACD,
∴∠ACD+∠FEC=90°,
∴∠EHC=90°,
∴EF⊥CD.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△ABE≌△CAM、△EFC≌△MCF和△ABE≌△ACD是解题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
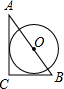 已知Rt△ABC中,∠C=90°,BC=a,AC=b,斜边AB上一点O为圆心,作⊙O使⊙O与直角边AC、BC都相切,则⊙O的半径r为( )
已知Rt△ABC中,∠C=90°,BC=a,AC=b,斜边AB上一点O为圆心,作⊙O使⊙O与直角边AC、BC都相切,则⊙O的半径r为( )A、
| ||
B、
| ||
C、
| ||
D、
|
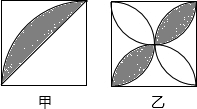 如图(甲)、(乙)是两个边长相等的正方形,甲图以边为半径在正方形内画圆弧,连接对角线;乙图以各边为直径在正方形内画半圆,阴影部分的面积分别记为S甲、S乙,那么S甲和S乙的大小关系是:S甲
如图(甲)、(乙)是两个边长相等的正方形,甲图以边为半径在正方形内画圆弧,连接对角线;乙图以各边为直径在正方形内画半圆,阴影部分的面积分别记为S甲、S乙,那么S甲和S乙的大小关系是:S甲 如图,等腰直角△ABC中,∠BAC=90°,AB=AC,点M、N在边BC上,且∠MAN=45°,MB=1,CN=3,求MN的长.
如图,等腰直角△ABC中,∠BAC=90°,AB=AC,点M、N在边BC上,且∠MAN=45°,MB=1,CN=3,求MN的长. 石家庄动物园和凤凰山是游客常去的两个景点,动物园(记作A)和凤凰山(记作B)位于笔直的石大高速公路1的同侧,如图所示,要在石大高速公路旁修建一服务区(记作P),向A,B两景点运送游客,并且要使从点P到A,B两地的路程和最短,则此服务区P应建在什么位置?请你用直尺和圆规在如图中画出你的设计方案.(保留作图痕迹,不要求写作法)
石家庄动物园和凤凰山是游客常去的两个景点,动物园(记作A)和凤凰山(记作B)位于笔直的石大高速公路1的同侧,如图所示,要在石大高速公路旁修建一服务区(记作P),向A,B两景点运送游客,并且要使从点P到A,B两地的路程和最短,则此服务区P应建在什么位置?请你用直尺和圆规在如图中画出你的设计方案.(保留作图痕迹,不要求写作法)