Question

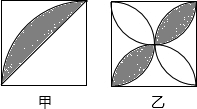如图（甲）、（乙）是两个边长相等的正方形，甲图以边为半径在正方形内画圆弧，连接对角线；乙图以各边为直径在正方形内画半圆，阴影部分的面积分别记为S_甲、S_乙，那么S_甲和S_乙的大小关系是：S_甲

 

S_乙．（填：“＞”、“═”或“＜”）

Answer 1

考点：扇形面积的计算

专题：

分析：设正方形的边长为a，根据S_甲=S_扇形-S_三角形=

1

4

π×a²-

1

2

a²，S_乙=

1

2

（四个半圆的面积-正方形的面积），再比较出其大小即可．

解答：解：设正方形的边长为a，
则S_甲=S_扇形-S_三角形=

1

4

π×a²-

1

2

a²=

1

4

a²π-

1

2

a²，
S_乙=

1

2

（四个半圆的面积-正方形的面积）
=

1

2

×（4×

1

2

π×

a2

4

-a²）
=

1

2

×（

1

2

a²π-a²）
=

1

4

a²π-

1

2

a²，
∴S_甲=S_乙．
故答案为：=．

点评：本题考查的是扇形的面积，熟知扇形的面积公式是解答此题的关键．