题目内容
解分式方程:
(1)
+
=
+
.
(2)
=
+
.
(3)
+2=
.
(1)
| 1 |
| x+1 |
| 1 |
| x+5 |
| 1 |
| x+2 |
| 1 |
| x+4 |
(2)
| 6 |
| x2-25 |
| 3 |
| x2+8x+15 |
| 5 |
| x2-2x-15 |
(3)
| 1-x |
| x-2 |
| 1 |
| x-2 |
考点:解分式方程
专题:计算题
分析:(1)方程两边通分并利用同分母分式的加法法则计算,即可确定出分式方程的解;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(3)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(3)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答:解:(1)分式方程变形得:
=
,
当2x+6=0,即x=-3时,满足方程;
当2x+6≠0,即x≠-3时,得到x2+6x=5=x2+6x+8,方程无解,
经检验x=-3是分式方程的解;
(2)去分母得:6x+18=3x-15+5x+25,
移项合并得:2x=8,
解得:x=4,
经检验x=4是分式方程的解;
(3)去分母得:1-x+2x-4=1,
解得:x=4,
经检验x=4是分式方程的解.
| 2x+6 |
| x2+6x+5 |
| 2x+6 |
| x2+6x+8 |
当2x+6=0,即x=-3时,满足方程;
当2x+6≠0,即x≠-3时,得到x2+6x=5=x2+6x+8,方程无解,
经检验x=-3是分式方程的解;
(2)去分母得:6x+18=3x-15+5x+25,
移项合并得:2x=8,
解得:x=4,
经检验x=4是分式方程的解;
(3)去分母得:1-x+2x-4=1,
解得:x=4,
经检验x=4是分式方程的解.
点评:此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
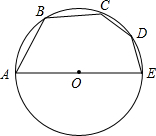 如图,AE是⊙O的直径,弦AB=BC=4
如图,AE是⊙O的直径,弦AB=BC=4| 2 |
| A、4 | ||
B、4
| ||
C、2
| ||
D、2
|
 甲、乙两车分别从相距200千米的A、B两地同时出发相向而行,甲到B地后立即返回A地,乙从B地直接到达A地,它们距A地的距离y(km)与行驶时间x(h)之间的函数图象如图所示.
甲、乙两车分别从相距200千米的A、B两地同时出发相向而行,甲到B地后立即返回A地,乙从B地直接到达A地,它们距A地的距离y(km)与行驶时间x(h)之间的函数图象如图所示. 在△ABC中,∠BAC=90°,AB=AC,∠ABC=∠ACB=45°,如图所示,点D、E分别是AB、AC边的中点,AF⊥BE交BC于点F,连结EF、CD交于点H.
在△ABC中,∠BAC=90°,AB=AC,∠ABC=∠ACB=45°,如图所示,点D、E分别是AB、AC边的中点,AF⊥BE交BC于点F,连结EF、CD交于点H. 如图,两个三角形摆成如图所示的形状,其中EC⊥BC于点C,点D在AC边上,DE∥BC,若∠1=155°,则∠2的度数为
如图,两个三角形摆成如图所示的形状,其中EC⊥BC于点C,点D在AC边上,DE∥BC,若∠1=155°,则∠2的度数为