题目内容
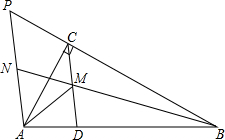 如图,△ABC中,∠ACB=90°,D是AB上一点,M是CD中点,且∠AMD=∠BMD,AP∥CD交BC延长线于P点,延长BM交PA于N点,且PN=AN.
如图,△ABC中,∠ACB=90°,D是AB上一点,M是CD中点,且∠AMD=∠BMD,AP∥CD交BC延长线于P点,延长BM交PA于N点,且PN=AN.(1)求证:MN=MA;
(2)求证:∠CDA=2∠ACD.
考点:相似三角形的判定与性质,全等三角形的判定与性质
专题:
分析:(1)由AP∥CD,得出∠AMD=∠MAN,∠BMD=∠MNA,由∠AMD=∠BMD,得出∠MAN=∠MNA,等角对等边得出MN=MA;
(2)连接NC,由AP∥CD,且PN=AN.可得MC=MD,由CN为直角△ACP斜边AP的中线,可得CN=NA,∠NCA=∠NAC,可得∠NCM=2∠ACD,再由△CMN≌△DMA,可得出∠ADM=∠NCM=2∠ACD.
(2)连接NC,由AP∥CD,且PN=AN.可得MC=MD,由CN为直角△ACP斜边AP的中线,可得CN=NA,∠NCA=∠NAC,可得∠NCM=2∠ACD,再由△CMN≌△DMA,可得出∠ADM=∠NCM=2∠ACD.
解答:证明:(1)∵AP∥CD,
∴∠AMD=∠MAN,∠BMD=∠MNA,
∵∠AMD=∠BMD,
∴∠MAN=∠MNA,
∴MN=MA.
(2)如图,连接NC,

∵AP∥CD,且PN=AN.
∴
=
=
,
∴MC=MD,
∴CN为直角△ACP斜边AP的中线,
∴CN=NA,∠NCA=∠NAC,
∵AP∥CD,
∴∠NAC=∠ACD,
∴∠NCM=2∠ACD,
∵∠CMN=∠DMB,∠DMA=∠BMD,
∴∠CMD=∠DMA,
在△CMN和△DMA中,
,
∴△CMN≌△DMA(SAS),
∠ADM=∠NCM=2∠ACD.即:∠CDA=2∠ACD.
∴∠AMD=∠MAN,∠BMD=∠MNA,
∵∠AMD=∠BMD,
∴∠MAN=∠MNA,
∴MN=MA.
(2)如图,连接NC,

∵AP∥CD,且PN=AN.
∴
| CM |
| PN |
| MD |
| NA |
| BM |
| BN |
∴MC=MD,
∴CN为直角△ACP斜边AP的中线,
∴CN=NA,∠NCA=∠NAC,
∵AP∥CD,
∴∠NAC=∠ACD,
∴∠NCM=2∠ACD,
∵∠CMN=∠DMB,∠DMA=∠BMD,
∴∠CMD=∠DMA,
在△CMN和△DMA中,
|
∴△CMN≌△DMA(SAS),
∠ADM=∠NCM=2∠ACD.即:∠CDA=2∠ACD.
点评:本题主要考查了相似三角形的判定与性质及全等三角形的判定与性质,解题的关键是正确作出辅助线,构造出全等三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
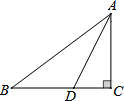 如图,Rt△ABC中,∠C=90°,AC=3,BC=4,AB=5,AD平分∠BAC.则S△ACD:S△ABD=( )
如图,Rt△ABC中,∠C=90°,AC=3,BC=4,AB=5,AD平分∠BAC.则S△ACD:S△ABD=( )| A、3:4 | B、3:5 |
| C、4:5 | D、1:1 |
 如图,在△ABC和△ADE中,
如图,在△ABC和△ADE中,