题目内容
在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,由下列条件解直角三角形.
(1)已知a=4
,c=8
;
(2)己知a=
,∠B=30°.
(1)已知a=4
| 10 |
| 5 |
(2)己知a=
| 6 |
考点:解直角三角形
专题:
分析:(1)根据勾股定理先求出b,再根据sinA=
,求出∠A,从而得出∠B;
(2)先求得∠B=90°-∠A,再根据∠B的余弦值求出c,由勾股定理得出b即可.
| a |
| c |
(2)先求得∠B=90°-∠A,再根据∠B的余弦值求出c,由勾股定理得出b即可.
解答:解:(1)∵∠C=90°,a=4
,c=8
,
∴b2=c2-a2=(8
)2-(4
)2
=320-160
=160,
∴b=4
,
∵sinA=
=
,
∴∠A=45°,
∴∠B=90°-∠A=90°-45°=45°;
(2)∵∠B=30°,
∴∠B=90°-∠A=90°-30°=60°,
∵a=
,
∴cosB=
=
,
∴c=2
,
∴b=
=
=
.
| 10 |
| 5 |
∴b2=c2-a2=(8
| 5 |
| 10 |
=320-160
=160,
∴b=4
| 10 |
∵sinA=
| a |
| c |
4
| ||
8
|
| ||
| 2 |
∴∠A=45°,
∴∠B=90°-∠A=90°-45°=45°;
(2)∵∠B=30°,
∴∠B=90°-∠A=90°-30°=60°,
∵a=
| 6 |
∴cosB=
| a |
| c |
| ||
| c |
∴c=2
| 2 |
∴b=
| c2-a2 |
(2
|
| 2 |
点评:本题考查了解直角三角形以及正弦和余弦的定义,是基础知识要熟练掌握.

练习册系列答案
相关题目
从一个多边形的任何一个顶点出发都只有5条对角线,则它的边数是( )
| A、6 | B、7 | C、8 | D、9 |
下列方程组中,是二元一次方程组的是( )
A、
| |||||||||
B、
| |||||||||
C、
| |||||||||
D、
|
 一块玻璃,AB∥CD,玻璃的板部分被打碎了,小华知道这块玻璃的高与CD相同,请画出打碎前的图形,并写出画法.
一块玻璃,AB∥CD,玻璃的板部分被打碎了,小华知道这块玻璃的高与CD相同,请画出打碎前的图形,并写出画法.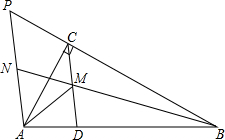 如图,△ABC中,∠ACB=90°,D是AB上一点,M是CD中点,且∠AMD=∠BMD,AP∥CD交BC延长线于P点,延长BM交PA于N点,且PN=AN.
如图,△ABC中,∠ACB=90°,D是AB上一点,M是CD中点,且∠AMD=∠BMD,AP∥CD交BC延长线于P点,延长BM交PA于N点,且PN=AN.