题目内容
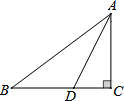 如图,Rt△ABC中,∠C=90°,AC=3,BC=4,AB=5,AD平分∠BAC.则S△ACD:S△ABD=( )
如图,Rt△ABC中,∠C=90°,AC=3,BC=4,AB=5,AD平分∠BAC.则S△ACD:S△ABD=( )| A、3:4 | B、3:5 |
| C、4:5 | D、1:1 |
考点:角平分线的性质
专题:
分析:过点D作DE⊥AB于点E,由角平分线的性质可得出DE=CD,由全等三角形的判定定理得出△ADC≌△ADE,故可得出AE的长,由AB=5求出BE的长,设CD=x,则DE=x,BD=4-x,再根据勾股定理求出x的值,进而可得出结论.
解答: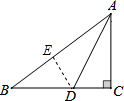 解:过点D作DE⊥AB于点E,
解:过点D作DE⊥AB于点E,
∵AD平分∠BAC,
∴DE=CD,
在Rt△ADC与Rt△ADE中,
,
∴△ADC≌△ADE(HL),
∴AE=AC=3,
∵AB=5,
∴BE=2.
设CD=x,则DE=x,BD=4-x,
在△BDE中,DE2+BE2=BD2,即x2+22=(4-x)2,解得x=
,
∴CD=
,BD=4-
=
,
∵△ACD与△ABD的高相等,
∴S△ACD:S△ABD=CD:BD=
:
=3:5.
故选B.
 解:过点D作DE⊥AB于点E,
解:过点D作DE⊥AB于点E,∵AD平分∠BAC,
∴DE=CD,
在Rt△ADC与Rt△ADE中,
|
∴△ADC≌△ADE(HL),
∴AE=AC=3,
∵AB=5,
∴BE=2.
设CD=x,则DE=x,BD=4-x,
在△BDE中,DE2+BE2=BD2,即x2+22=(4-x)2,解得x=
| 3 |
| 2 |
∴CD=
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
∵△ACD与△ABD的高相等,
∴S△ACD:S△ABD=CD:BD=
| 3 |
| 2 |
| 5 |
| 2 |
故选B.
点评:本题考查的是角平分线的性质,熟知角平分线上的点到角两边的距离相等是解答此题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
下列各数中,是无理数的是( )
| A、7 | ||
| B、0.5 | ||
C、
| ||
| D、0.5151151115…(两个5个之间依次多个1) |
从一个多边形的任何一个顶点出发都只有5条对角线,则它的边数是( )
| A、6 | B、7 | C、8 | D、9 |
已知点A(-1,y1)、B(1,y2)在直线y=-2x+3上,则y1与y2的大小关系是( )
| A、y1>y2 |
| B、y1<y2 |
| C、yl=y2 |
| D、y1与y2的大小关系不确定 |
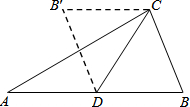 如图,在△ABC中,已知AB=2a,∠A=30°,CD是AB边的中线,若将△ABC沿CD对折起来,折叠后两个小△ACD与△BCD重叠部分的面积恰好等于折叠前△ABC的面积的
如图,在△ABC中,已知AB=2a,∠A=30°,CD是AB边的中线,若将△ABC沿CD对折起来,折叠后两个小△ACD与△BCD重叠部分的面积恰好等于折叠前△ABC的面积的| 1 |
| 4 |
①BC的边长等于a;
②折叠前的△ABC的面积可以等于
| ||
| 2 |
③折叠前的△ABC的面积可以等于
| ||
| 3 |
④折叠后,以A、B为端点的线段与中线CD一定平行且相等.
其中正确的结论是( )
| A、①③ | B、①②④ |
| C、①③④ | D、①②③④ |
 如图,点P是正方形ABCD的BC边上一动点,PE⊥BD于E,PF⊥AC于F,若AC=12,则PE+PF的值是( )
如图,点P是正方形ABCD的BC边上一动点,PE⊥BD于E,PF⊥AC于F,若AC=12,则PE+PF的值是( )| A、6 | ||
| B、10 | ||
C、6
| ||
| D、12 |
下列方程组中,是二元一次方程组的是( )
A、
| |||||||||
B、
| |||||||||
C、
| |||||||||
D、
|
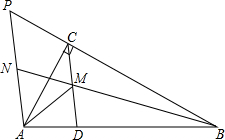 如图,△ABC中,∠ACB=90°,D是AB上一点,M是CD中点,且∠AMD=∠BMD,AP∥CD交BC延长线于P点,延长BM交PA于N点,且PN=AN.
如图,△ABC中,∠ACB=90°,D是AB上一点,M是CD中点,且∠AMD=∠BMD,AP∥CD交BC延长线于P点,延长BM交PA于N点,且PN=AN.