题目内容
2.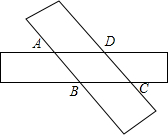 如图,两张宽为1cm的矩形纸条交叉叠放,其中重叠部分部分是四边形ABCD,
如图,两张宽为1cm的矩形纸条交叉叠放,其中重叠部分部分是四边形ABCD,(1)试判断四边形ABCD的形状,并说明理由
(2)若∠BAD=30°,求重叠部分的面积.
分析 (1)考查菱形的判定,四条边相等的四边形即为菱形;
(2)要求重叠部分的面积,根据面积公式,求出底和高即可.可以通过作辅助线求得.
解答 解:(1)四边形ABCD是菱形,
理由是:如图1所示:
∵依题意可知AB∥CD,AD∥BC,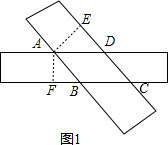
∴四边形ABCD是平行四边形,
分别作CD,BC边上的高为AE,AF,
∵两纸条相同,
∴纸条宽度AE=AF,
∵平行四边形的面积为AE×CD=BC×AF,
∴CD=BC,
∴平行四边形ABCD为菱形;
(2)如图2所示,过B、D两点分别作BE⊥AD、DF⊥AB,垂足分别为E、F,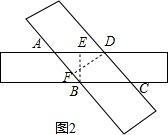
∵宽为1cm,
∴BE=DF=1cm,
∵∠BAD=30°,
∴AB=2cm,
∴重叠部分的面积为DF×B=1×2=2cm2.
点评 本题考查了菱形的性质和判定,面积公式的综合运用,能正确作出辅助线是解此题的关键.

练习册系列答案
相关题目
13.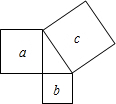 如图,a、b、c分别表示直角三角形的三边向外作的正方形的面积,下列关系正确的是( )
如图,a、b、c分别表示直角三角形的三边向外作的正方形的面积,下列关系正确的是( )
 如图,a、b、c分别表示直角三角形的三边向外作的正方形的面积,下列关系正确的是( )
如图,a、b、c分别表示直角三角形的三边向外作的正方形的面积,下列关系正确的是( )| A. | a+b=c | B. | a2+b2=c2 | C. | ab=c | D. | a+b=c2 |
7.如图是本地区一种产品30天的销售图象,图①是产品日销售量y(单位:件)与时间t(单位;天)的函数关系,图②是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列结论错误的是( )
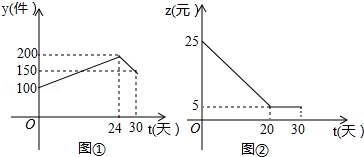

| A. | 第24天的销售量最多 | |
| B. | 20≤t≤30日销售利润不变 | |
| C. | 第30天的日销售利润是750元 | |
| D. | 当0≤t≤24时,设产品日销售量y与时间t的函数关系为y=$\frac{25}{6}$t+100 |
 如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以边上AC上一点O为圆心,OA为半径作⊙O,⊙O恰好经过边BC的中点D,并与边AC相交于另一点F.
如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以边上AC上一点O为圆心,OA为半径作⊙O,⊙O恰好经过边BC的中点D,并与边AC相交于另一点F. 平移三角形ABC,使点A移动到点A′,画出平移后的△A′B′C′.若AB=3cm,则A′B′=3cm;若∠C′=45°,则∠C=45°.
平移三角形ABC,使点A移动到点A′,画出平移后的△A′B′C′.若AB=3cm,则A′B′=3cm;若∠C′=45°,则∠C=45°.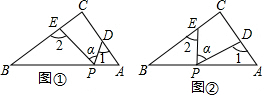
 如图,则∠A+∠B+∠C+∠D+∠E+∠F的度数为360度.
如图,则∠A+∠B+∠C+∠D+∠E+∠F的度数为360度.