题目内容
14．一个正多边形的每个内角比相邻的外角大36°，求这个多边形的边数．分析 首先设内角为x°，则外角为（x-36）°，根据内角与相邻外角和为180°可得方程x+x-36=180，计算出x的值，进而可得外角的度数，然后可得多边形的边数．
解答 解：设内角为x°，则外角为（x-36）°，由题意得：
x+x-36=180，
解得：x=108，
则外角为108°-36°=72°，
多边形的边数：360°÷72°=5．
点评 此题主要考查了多边形的内角与外角，关键是掌握内角与相邻外角和为180．
练习册系列答案
阅读快车系列答案
相关题目
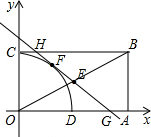如图，在平面直角坐标系中，矩形OABC的顶点O在坐标原点，顶点A、C分别在x轴、y轴的正半轴上，且OA=2，OC=1，矩形对角线AC、OB相交于E，过点E的直线与边OA、BC分别相交于点G、H，以O为圆心，OC为半径的圆弧交OA于D，若直线GH与弧CD所在的圆相切于矩形内一点F，则下列结论：①AG=CH；②GH=$\frac{5}{3}$；③直线GH的函数关系式y=-$\frac{3}{4}x+\frac{5}{4}$；④梯形ABHG的内部有一点P，当⊙P与HG、GA、AB都相切时，⊙P的半径为$\frac{1}{4}$．其中正确的有（ ）
5．下列各组数中互为相反数的一组数是（ ）
| A． | |-2|与2 | B． | -2与-$\frac{1}{2}$ | C． | -2与$\root{3}{-8}$ | D． | -3与$\sqrt{（-3）^{2}}$ |
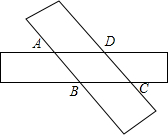如图，两张宽为1cm的矩形纸条交叉叠放，其中重叠部分部分是四边形ABCD，
9．下列等式正确的是（ ）
| A． | （-x2）3=-x5 | B． | x3+x3=2x6 | C． | a3•a3=2a3 | D． | 26+26=27 |
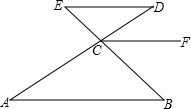如图：已知∠A=∠D，∠B=∠FCB，能否确定ED与CF的位置关系，
3．将二次函数y=x2+1的图象向右平移1个单位，则平移后的二次函数的解析式为（ ）
| A． | y=x2 | B． | y=（x-1）2 | C． | y=（x-1）2+1 | D． | y=（x+1）2+1 |