题目内容
20.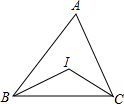 如图,△ABC中,∠A=45°,I是内心,则∠BIC=115°.
如图,△ABC中,∠A=45°,I是内心,则∠BIC=115°.
分析 由三角形内切定义可知:IB、IC是∠ABC、∠ACB的角平分线,所以可得到关系式∠IBC+∠ICB=$\frac{1}{2}$(∠ABC+∠ACB),把对应数值代入即可解出∠BIC的值.
解答 解:∵IB、IC是∠ABC、∠ACB的角平分线,
∴∠IBC+∠ICB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$(180°-50°)=65°,
∴∠BIC=180°-65°=115°.
故答案为:115.
点评 本题是三角形内切圆与内心,主要考查三角形的内心是内角平分线的交点.解题关键是要会找到关系式∠IBC+∠ICB=$\frac{1}{2}$(∠ABC+∠ACB).

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
9.已知点A(a,-b)在第二象限,则点B(a-3,b-2)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
5.下列说法正确的是( )
| A. | -33a2bc2的系数为-3,次数为27 | B. | $\frac{x}{π}$+$\frac{y}{2}$+$\frac{{z}^{2}}{3}$不是单项式,但是整式 | ||
| C. | $\frac{1}{x+1}$是多项式 | D. | mx2+1一定是关于x的二次二项式 |
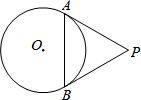 如图,PA、PB分别与相切⊙O于点A、B,连接AB.∠APB=60°,AB=5,则⊙O的半径长为2$\sqrt{3}$.
如图,PA、PB分别与相切⊙O于点A、B,连接AB.∠APB=60°,AB=5,则⊙O的半径长为2$\sqrt{3}$.