题目内容
18．
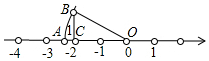已知，如图，OA=OB，那么数轴上的点A所表示的数是（ ）| A． | $\sqrt{3}$ | B． | $\sqrt{5}$ | C． | -$\sqrt{5}$ | D． | -$\sqrt{7}$ |
分析 首先根据勾股定理得：OB=$\sqrt{5}$．即OA=$\sqrt{5}$．又点A在数轴的负半轴上，则点A对应的数是-$\sqrt{5}$．
解答 解：由图可知，OC=2，作BC⊥OC，垂足为C，取BC=1，
故OB=OA=$\sqrt{O{C}^{2}+B{C}^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$，
∵A在x的负半轴上，
∴数轴上点A所表示的数是-$\sqrt{5}$，
故选C．
点评 本题考查了实数与数轴，熟练运用勾股定理，同时注意根据点的位置以确定数的符号．
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
如图，长方体的长、宽、高分别是9cm，7cm，8cm，一只蚂蚁沿着长方体的表面从点A爬到点B，则蚂蚁爬行的最短路径长$\sqrt{296}$．
9．已知点A（a，-b）在第二象限，则点B（a-3，b-2）在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
6．不等式4-2x＞0的最大正整数解是（ ）
| A． | 4 | B． | 3 | C． | 2 | D． | 1 |
13．下列说法错误的是（ ）
| A． | 42的算术平方根为4 | B． | 2的算术平方根为$\sqrt{2}$ | ||
| C． | $\sqrt{{3}^{2}}$的算术平方根是$\sqrt{3}$ | D． | $\sqrt{81}$的算术平方根是9 |
3．下列四个几何图形中，俯视图是矩形的是（ ）
| A． |  | B． |  | C． |  | D． |  |