题目内容
3.如图,线段AB是⊙O的直径,BC⊥CD于点C,AD⊥CD于点D,请仅用无刻度的直尺按下列要求作图.(1)在图1中,当线段CD与⊙O相切时,请在CD上确定一点E,连接BE,使BE平分∠ABC;
(2)在图2中,当线段CD与⊙O相离时,请过点O作OF⊥CD,垂足为F.
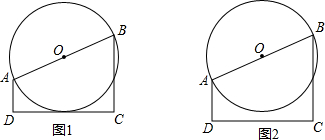
分析 (1)构造矩形ADCM,对角相等交点为H,连接OH,延长OH交CD于E,连接BE,射线BE即为所求作.
(2)方法类似(1).
解答 解:(1)如图1中,设BC交⊙O于M,连接AM、AC、DM,AC与DM交于点H,连接OH,延长OH交CD于点E,连接BE,BE即为所求作.
(2)如图2中,
设BC交⊙O于M,连接AM、AC、DM,AC与DM交于点H,连接OH,延长OH交CD于点F,则OF⊥CD于F.
点评 本题考查切线的性质、垂径定理、矩形的性质和判定、垂直平分线的性质和判定、角平分线的判定等知识,解题的关键是灵活运用这些知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
13.下列说法错误的是( )
| A. | 42的算术平方根为4 | B. | 2的算术平方根为$\sqrt{2}$ | ||
| C. | $\sqrt{{3}^{2}}$的算术平方根是$\sqrt{3}$ | D. | $\sqrt{81}$的算术平方根是9 |
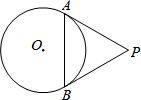 如图,PA、PB分别与相切⊙O于点A、B,连接AB.∠APB=60°,AB=5,则⊙O的半径长为2$\sqrt{3}$.
如图,PA、PB分别与相切⊙O于点A、B,连接AB.∠APB=60°,AB=5,则⊙O的半径长为2$\sqrt{3}$.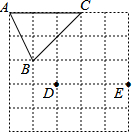 如图是5×5的正方形网格,以格点D、E为两个顶点作位置不同的格点三角形,使所作的格点三角形与△ABC全等,这样的格点三角形最多可以作出( )
如图是5×5的正方形网格,以格点D、E为两个顶点作位置不同的格点三角形,使所作的格点三角形与△ABC全等,这样的格点三角形最多可以作出( )