题目内容
15. 如图,菱形OABC的顶点O为坐标原点,顶点A在x轴正半轴上,顶点B、C在第一象限,OA=2,∠AOC=60°,点D在边AB上,将四边形ODBC沿直线OD翻折,使点B和点C分别落在这个坐标平面内的B′和C′处,且∠C′DB′=60°,某正比例函数图象经过B′,则这个正比例函数的解析式为( )
如图,菱形OABC的顶点O为坐标原点,顶点A在x轴正半轴上,顶点B、C在第一象限,OA=2,∠AOC=60°,点D在边AB上,将四边形ODBC沿直线OD翻折,使点B和点C分别落在这个坐标平面内的B′和C′处,且∠C′DB′=60°,某正比例函数图象经过B′,则这个正比例函数的解析式为( )| A. | y=-$\frac{\sqrt{3}}{2}$x | B. | y=-$\frac{\sqrt{3}}{3}x$ | C. | y=-$\frac{1}{2}x$ | D. | y=-x |
分析 连接AC,求出△BAC是等边三角形,推出AC=AB,求出△DC′B′是等边三角形,推出C′D=B′D,得出CB=BD=B′C′,推出A和D重合,连接BB′交x轴于E,求出AB′=AB=2,∠B′AE=60°,求出B′的坐标即可求得正比例函数的解析式.
解答 解:连接AC,
∵四边形OABC是菱形,
∴CB=AB,∠CBA=∠AOC=60°,
∴△BAC是等边三角形,
∴AC=AB,
∵将四边形OABC沿直线0D翻折,使点B和点C分别落在这个坐标平面的点B′和C′处,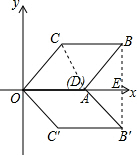
∴BD=B′D,CD=C′D,∠DB′C′=∠ABC=60°,
∵∠B′DC′=60°,
∴∠DC′B′=60°,
∴△DC′B′是等边三角形,
∴C′D=B′D,
∴CB=BD=B′C′,
即A和D重合,
连接BB′交x轴于E,
则AB′=AB=2,∠B′AE=180°-(180°-60°)=60°,
在Rt△AB′E中,∠B′AE=60°,AB′=2,
∴AE=1,B′E=$\sqrt{3}$,OE=2+1=3,
即B′的坐标是(3,-$\sqrt{3}$),
设正比例函数的解析式为y=kx,
∵正比例函数图象经过B′,
∴-$\sqrt{3}$=3k,
∴k=-$\frac{\sqrt{3}}{3}$.
故选B.
点评 本题考查了折叠性质,菱形性质,等边三角形的性质和判定的应用,主要考查学生的计算能力,题目比较好,有一定的难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3. 已知甲、乙两个班的人数在扇形统计图中所占的比例如图所示,甲班有55人,则乙班人数是( )
已知甲、乙两个班的人数在扇形统计图中所占的比例如图所示,甲班有55人,则乙班人数是( )
 已知甲、乙两个班的人数在扇形统计图中所占的比例如图所示,甲班有55人,则乙班人数是( )
已知甲、乙两个班的人数在扇形统计图中所占的比例如图所示,甲班有55人,则乙班人数是( )| A. | 60人 | B. | 62人 | C. | 64人 | D. | 66人 |
10.若二次函数y=kx2-kx+1与x轴有两个交点.则k的取值范围是( )
| A. | k>4或k<0 | B. | 0<k<4 | C. | k≥4或k≤0 | D. | 0≤k≤4 |
7.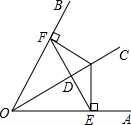 如图,已知OC平分∠AOB,CE⊥OA于E,CF⊥OB于F,EF交OC于D,则下列结论:
如图,已知OC平分∠AOB,CE⊥OA于E,CF⊥OB于F,EF交OC于D,则下列结论:
①OE=OF,②OD=CD,③EF⊥OC,④∠OEF=∠CEF,⑤图中共有3对全等三角形;其中正确的有( )
 如图,已知OC平分∠AOB,CE⊥OA于E,CF⊥OB于F,EF交OC于D,则下列结论:
如图,已知OC平分∠AOB,CE⊥OA于E,CF⊥OB于F,EF交OC于D,则下列结论:①OE=OF,②OD=CD,③EF⊥OC,④∠OEF=∠CEF,⑤图中共有3对全等三角形;其中正确的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
4.利用乘法分配律计算(-10$\frac{8}{9}$)×9时,正确的方法( )
| A. | (-11-$\frac{8}{9}$)×9=-11×9-$\frac{8}{9}$×9 | B. | (-10-$\frac{8}{9}$)×9=-10×9-$\frac{8}{9}$×9 | ||
| C. | (10-$\frac{8}{9}$)×9=10×9-$\frac{8}{9}$×9 | D. | -(10-$\frac{8}{9}$)×9=-(10×9-$\frac{8}{9}$×9) |