题目内容
5．求下列各数的立方根（1）-0.001；
（2）3$\frac{3}{8}$；
（3）（-4）3．
分析 根据立方根的计算方法可以解答本题．
解答 解：（1）$\root{3}{-0.001}=-0.1$；
（2）$\root{3}{3\frac{3}{8}}=\root{3}{\frac{27}{8}}=\frac{3}{2}$；
（3）$\root{3}{（-4）^{3}}=-4$．
点评 本题考查立方根，解题的关键是明确立方根的计算方法．
练习册系列答案
名校课堂系列答案
相关题目
16．下列说法：
①0是自然数，是整数，是非负数；
②$-\frac{22}{7}$是负数又是分数，但不是有理数；
③-1是最大的负整数；
④几个有理数相乘，如果负因数的个数为奇数个，则积为负；
⑤一个数的绝对值是它的本身，则这个数是正数；
其中错误的有（ ）
①0是自然数，是整数，是非负数；
②$-\frac{22}{7}$是负数又是分数，但不是有理数；
③-1是最大的负整数；
④几个有理数相乘，如果负因数的个数为奇数个，则积为负；
⑤一个数的绝对值是它的本身，则这个数是正数；
其中错误的有（ ）
| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
10．
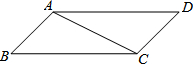如图，△ABC≌△CDA，且AB、CD是对应边，下面四个结论中不正确的是（ ）
如图，△ABC≌△CDA，且AB、CD是对应边，下面四个结论中不正确的是（ ）| A． | △ABC和△CDA的面积相等 | B． | △ABC和△CDA的周长相等 | ||
| C． | ∠B+∠BAC=∠D+∠DAC | D． | AD=BC |
15．
如图，菱形OABC的顶点O为坐标原点，顶点A在x轴正半轴上，顶点B、C在第一象限，OA=2，∠AOC=60°，点D在边AB上，将四边形ODBC沿直线OD翻折，使点B和点C分别落在这个坐标平面内的B′和C′处，且∠C′DB′=60°，某正比例函数图象经过B′，则这个正比例函数的解析式为（ ）
如图，菱形OABC的顶点O为坐标原点，顶点A在x轴正半轴上，顶点B、C在第一象限，OA=2，∠AOC=60°，点D在边AB上，将四边形ODBC沿直线OD翻折，使点B和点C分别落在这个坐标平面内的B′和C′处，且∠C′DB′=60°，某正比例函数图象经过B′，则这个正比例函数的解析式为（ ）| A． | y=-$\frac{\sqrt{3}}{2}$x | B． | y=-$\frac{\sqrt{3}}{3}x$ | C． | y=-$\frac{1}{2}x$ | D． | y=-x |