题目内容
11.△ABC中,∠C=90°,CD是高,AB=10,则2CD2+AD2+BD2=100.分析 由勾股定理得出AB2=AC2+BC2,AC2=AD2+CD2,BC2=CD2+DB2,得出AB2=AD2+CD2+CD2+DB2,即可2CD2+AD2+BD2的值.
解答  解:
解:
∵∠ACB=90°,
∴AB2=AC2+BC2,
∵CD⊥AB,
∴∠ADC=∠BDC=90°,
∴AC2=AD2+CD2,BC2=CD2+DB2,
∴AB2=AD2+CD2+CD2+DB2=AD2+DB2+2CD2,
∵AB=10,
∴2CD2+AD2+BD2=100,
故答案为:100.
点评 本题考查了勾股定理;熟练掌握勾股定理,在三个直角三角形中运用勾股定理得出AB2=AD2+CD2+CD2+DB2是解决问题的关键

练习册系列答案
相关题目
1.x=3是下列哪个方程的解( )
| A. | 2x+6=11 | B. | 6x-5=3x+4 | C. | 3x=$\frac{1}{3}$ | D. | -x=3 |
19.若a,b是互为相反数(a≠0),则关于x的一元一次方程ax+b=0的解是( )
| A. | 1 | B. | -1 | C. | -1或1 | D. | 任意有理数 |
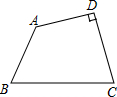 如图,在四边形ABCD中,∠D=90°,AB=2,BC=4,CD=AD=$\sqrt{6}$.
如图,在四边形ABCD中,∠D=90°,AB=2,BC=4,CD=AD=$\sqrt{6}$.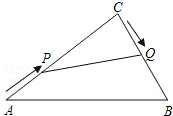 在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm.现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动.如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动,设运动的时间为t秒.求:
在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm.现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动.如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动,设运动的时间为t秒.求: