题目内容
1．
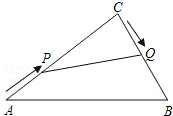在Rt△ABC中，∠C=90°，AC=20cm，BC=15cm．现有动点P从点A出发，沿AC向点C方向运动，动点Q从点C出发，沿线段CB也向点B方向运动．如果点P的速度是4cm/秒，点Q的速度是2cm/秒，它们同时出发，当有一点到达所在线段的端点时，就停止运动，设运动的时间为t秒．求：（1）用含t的代数式表示Rt△CPQ的面积S；
（2）当t=3秒时，P、Q两点之间的距离是多少？
分析 （1）由点P，点Q的运动速度和运动时间，又知AC，BC的长，可将CP、CQ用含t的表达式求出，代入直角三角形面积公式S△CPQ=$\frac{1}{2}$CP×CQ求解；
（2）在Rt△CPQ中，由（1）可知CP、CQ的长，运用勾股定理可将PQ的长求出．
解答 解：（1）由题意得AP=4t，CQ=2t，则CP=20-4t，
∴Rt△CPQ的面积为S=$\frac{1}{2}$（20-2t）×2t=20t-4t2（cm2）；
（2）当t=3秒时，CP=20-4t=8cm，CQ=2t=6cm，
在Rt△PCQ中，由勾股定理得：PQ=$\sqrt{C{P}^{2}+C{Q}^{2}}$=10cm．
点评 本题主要考查勾股定理以及三角形面积的计算；熟练掌握勾股定理是解决问题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
方程术是《九章算术》最高的数学成就，《九章算术》中“盈不足”一章中记载：“今有大器五小器一容三斛（古代的一种容量单位），大器一小器五容二斛，…”译文：“已知5个大桶加上1个小桶可以盛酒3斛，1个大桶加上5个小桶可以盛酒2斛，…”则一个大桶和一个小桶一共可以盛酒$\frac{5}{6}$斛．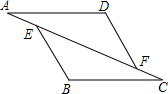
如图，已知：在△AFD和△CEB中，点A、E、F、C在同一直线上，AE=CF，∠B=∠D，AD∥BC，若AD+BC=10，则AD的长是（ ）
10．抛物线y=2（x+1）2+1的顶点坐标是（ ）
| A． | （1，1） | B． | （1，-1） | C． | （-1，1） | D． | （-1，-1） |
