题目内容
4.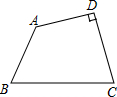 如图,在四边形ABCD中,∠D=90°,AB=2,BC=4,CD=AD=$\sqrt{6}$.
如图,在四边形ABCD中,∠D=90°,AB=2,BC=4,CD=AD=$\sqrt{6}$.(1)求∠BAD、∠BCD的度数.
(2)求四边形ABCD的面积.
分析 (1)由等腰直角三角形的性质得出∠DAC=∠ACD=45°,AC2=AD2+CD2=2×6=12.AC=2$\sqrt{3}$,由勾股定理的逆定理证出∠BAC=90°.证出∠ACB=30°,即可得出所求;
(2)四边形ABCD的面积=△ABC的面积+△ACD的面积,代入计算即可.
解答 解:(1)连接AC,如图所示: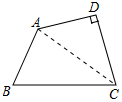
∵CD=AD=$\sqrt{6}$,∠D=90°,
∴∠DAC=∠ACD=45°,AC2=AD2+CD2=2×6=12.AC=2$\sqrt{3}$,
在△ABC中,∵AB2+BC2=22+12=16=AC2,
∴∠BAC=90°.
∵BC=2AB,
∴∠ACB=30°,
∴∠BAD=∠BAC+∠CAD=90°+45°=135°,∠BCD=∠ACB+∠ACD=30°+45°=75°;
(2)四边形ABCD的面积=△ABC的面积+△ACD的面积$\frac{1}{2}$×2×2$\sqrt{3}$+$\frac{1}{2}$×$\sqrt{6}$×$\sqrt{6}$=2$\sqrt{3}$+3.
点评 此题考查了勾股定理,等腰直角三角形的性质、勾股定理的逆定理以及含30°直角三角形的性质,熟练掌握勾股定理和逆定理是解本题的关键.

练习册系列答案
相关题目
 方程术是《九章算术》最高的数学成就,《九章算术》中“盈不足”一章中记载:“今有大器五小器一容三斛(古代的一种容量单位),大器一小器五容二斛,…”译文:“已知5个大桶加上1个小桶可以盛酒3斛,1个大桶加上5个小桶可以盛酒2斛,…”则一个大桶和一个小桶一共可以盛酒$\frac{5}{6}$斛.
方程术是《九章算术》最高的数学成就,《九章算术》中“盈不足”一章中记载:“今有大器五小器一容三斛(古代的一种容量单位),大器一小器五容二斛,…”译文:“已知5个大桶加上1个小桶可以盛酒3斛,1个大桶加上5个小桶可以盛酒2斛,…”则一个大桶和一个小桶一共可以盛酒$\frac{5}{6}$斛.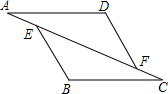 如图,已知:在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,∠B=∠D,AD∥BC,若AD+BC=10,则AD的长是( )
如图,已知:在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,∠B=∠D,AD∥BC,若AD+BC=10,则AD的长是( )