题目内容
3.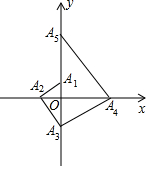 如图,点A1的坐标为(0,1),A2在x轴的负半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交y轴于点A3;过点A3作A3A4⊥A2A3,垂足为A3,交x轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交y轴于点A5;…按此规律进行下去,则点A2017的坐标为(0,31008).
如图,点A1的坐标为(0,1),A2在x轴的负半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交y轴于点A3;过点A3作A3A4⊥A2A3,垂足为A3,交x轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交y轴于点A5;…按此规律进行下去,则点A2017的坐标为(0,31008).
分析 由∠A1A2O=30°结合点A1的坐标即可得出点A2的坐标,由A2A3⊥A1A2结合点A2的坐标即可得出点A3的坐标,同理找出点A4、A5、A6、…的坐标,根据坐标的变化找出变化规律“A4n+1(0,($\sqrt{3}$)4n),A4n+2((-$\sqrt{3}$)4n+1,0),A4n+3(0,-($\sqrt{3}$)4n+2),A4n+4(($\sqrt{3}$)4n+3,0)(n为自然数)”,依此规律结合2017=504×4+1即可得出点A2017的坐标,此题得解..
解答 解:∵∠A1A2O=30°,点A1的坐标为(0,1),
∴点A2的坐标为(-$\sqrt{3}$,0).
∵A2A3⊥A1A2,
∴点A3的坐标为(0,-3).
同理可得:A4(3$\sqrt{3}$,0),A5(0,9),A6(-9$\sqrt{3}$,0),…,
∴A4n+1(0,($\sqrt{3}$)4n),A4n+2((-$\sqrt{3}$)4n+1,0),
A4n+3(0,-($\sqrt{3}$)4n+2),A4n+4(($\sqrt{3}$)4n+3,0)(n为自然数).
∵2017=504×4+1,
∴A2017(0,($\sqrt{3}$)2016),
即A2017(0,31008),
故答案为(0,31008).
点评 本题考查了规律型中点的坐标以及含30度角的直角三角形,根据点的变化找出变化规律,是解题的关键.

练习册系列答案
相关题目
20.2017的相反数是( )
| A. | -2017 | B. | 2017 | C. | $\frac{1}{2017}$ | D. | -$\frac{1}{2017}$ |
1.已知a、b、c为常数,点P(a,c)在第二象限,则关于x的方程ax2+bx+c=0根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 没有实数根 | D. | 无法判断 |
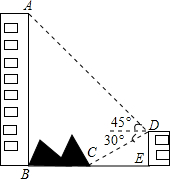 如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=60m,DE=10m,求障碍物B,C两点间的距离(结果精确到0.1m)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=60m,DE=10m,求障碍物B,C两点间的距离(结果精确到0.1m)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)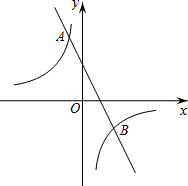 如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=-2x+1交于点A(-1,a)
如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=-2x+1交于点A(-1,a)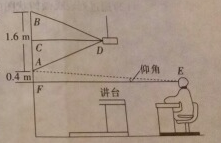 教室的屏幕AB、投影仪D及教室中间前排学生位置左视图如图所示,为了确保眼睛不易疲劳,安装时要求教室中间前排学生与屏幕的距离≥屏幕高度的2倍.现测得屏幕的高度AB=1.6m,在屏幕的正中央C的前方放的投影仪离屏幕的距离CD=2m,前排学生的眼睛E看屏幕底端A的仰角∠AEF=6°,屏幕底端A到水平线EF的距离AF=0.4m.
教室的屏幕AB、投影仪D及教室中间前排学生位置左视图如图所示,为了确保眼睛不易疲劳,安装时要求教室中间前排学生与屏幕的距离≥屏幕高度的2倍.现测得屏幕的高度AB=1.6m,在屏幕的正中央C的前方放的投影仪离屏幕的距离CD=2m,前排学生的眼睛E看屏幕底端A的仰角∠AEF=6°,屏幕底端A到水平线EF的距离AF=0.4m.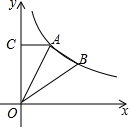 如图,O为坐标原点,A、B是函数y=$\frac{9\sqrt{2}}{x}$(x>0)的图象上的两点,过A作AC⊥y轴于C,若AB⊥OA,且△OAB与△ACO相似,则点B的坐标为(6,$\frac{3\sqrt{2}}{2}$).
如图,O为坐标原点,A、B是函数y=$\frac{9\sqrt{2}}{x}$(x>0)的图象上的两点,过A作AC⊥y轴于C,若AB⊥OA,且△OAB与△ACO相似,则点B的坐标为(6,$\frac{3\sqrt{2}}{2}$).