题目内容
13.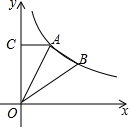 如图,O为坐标原点,A、B是函数y=$\frac{9\sqrt{2}}{x}$(x>0)的图象上的两点,过A作AC⊥y轴于C,若AB⊥OA,且△OAB与△ACO相似,则点B的坐标为(6,$\frac{3\sqrt{2}}{2}$).
如图,O为坐标原点,A、B是函数y=$\frac{9\sqrt{2}}{x}$(x>0)的图象上的两点,过A作AC⊥y轴于C,若AB⊥OA,且△OAB与△ACO相似,则点B的坐标为(6,$\frac{3\sqrt{2}}{2}$).
分析 根据相似三角形的性质得到∠AOC=∠BOA,得到OA是∠BOC的平分线,延长BA交y轴于D,过B作BE⊥y轴于E,得到AC∥BE,设A(a,$\frac{9\sqrt{2}}{a}$),根据射影定理得到CD=$\frac{{a}^{3}}{9\sqrt{2}}$,根据三角形的中位线的性质得到B(2a,$\frac{9\sqrt{2}}{a}$-$\frac{{a}^{3}}{9\sqrt{2}}$),列方程即可得到结论.
解答  解:∵△OAB∽△ACO,
解:∵△OAB∽△ACO,
∴∠AOC=∠BOA,
∴OA是∠BOC的平分线,
延长BA交y轴于D,过B作BE⊥y轴于E,
∵AC⊥OC,
∴AC∥BE,
∵AB⊥OA,
∴AB=AD,
设A(a,$\frac{9\sqrt{2}}{a}$),
∴AC2=CD•OA,
∴CD=$\frac{{a}^{3}}{9\sqrt{2}}$,
∴CE=CD=$\frac{{a}^{3}}{9\sqrt{2}}$,
∴OE=$\frac{9\sqrt{2}}{a}$-$\frac{{a}^{3}}{9\sqrt{2}}$,
BE=2AC=2a,
∴B(2a,$\frac{9\sqrt{2}}{a}$-$\frac{{a}^{3}}{9\sqrt{2}}$),
∴2a($\frac{9\sqrt{2}}{a}$-$\frac{{a}^{3}}{9\sqrt{2}}$)=9$\sqrt{2}$,
解得:a=3,(负值舍去),
∴点B的坐标为(6,$\frac{3\sqrt{2}}{2}$).
故答案为:(6,$\frac{3\sqrt{2}}{2}$).
点评 本题考查了相似三角形的性质,反比例函数图象上点的坐标特征,射影定理,正确的作出辅助线是解题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
3.按照一定规律排列的n个数:-2、4、-8、16、-32、64、…,若最后三个数的和为768,则n为( )
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
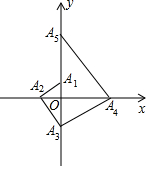 如图,点A1的坐标为(0,1),A2在x轴的负半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交y轴于点A3;过点A3作A3A4⊥A2A3,垂足为A3,交x轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交y轴于点A5;…按此规律进行下去,则点A2017的坐标为(0,31008).
如图,点A1的坐标为(0,1),A2在x轴的负半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交y轴于点A3;过点A3作A3A4⊥A2A3,垂足为A3,交x轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交y轴于点A5;…按此规律进行下去,则点A2017的坐标为(0,31008).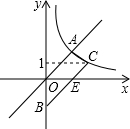 如图,梯形AOBC的顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x上,下底边BC交y轴于B(0,-4),则四边形AOBC的面积为2$\sqrt{5}$+10.
如图,梯形AOBC的顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x上,下底边BC交y轴于B(0,-4),则四边形AOBC的面积为2$\sqrt{5}$+10.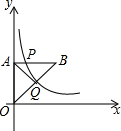 如图,平面直角坐标系中,O为坐标原点,等腰Rt△OAB的顶点B在第一象限,直角边OA在y轴上,点P是边AB上的一个三等分点,过点P的反比例函数y=$\frac{k}{x}$的图象交斜边OB于点Q,△AOQ的面积为3,则k的值为2$\sqrt{3}$或2$\sqrt{6}$.
如图,平面直角坐标系中,O为坐标原点,等腰Rt△OAB的顶点B在第一象限,直角边OA在y轴上,点P是边AB上的一个三等分点,过点P的反比例函数y=$\frac{k}{x}$的图象交斜边OB于点Q,△AOQ的面积为3,则k的值为2$\sqrt{3}$或2$\sqrt{6}$. 阅读下面材料:
阅读下面材料: