题目内容
8.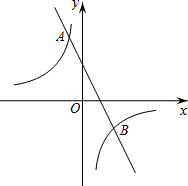 如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=-2x+1交于点A(-1,a)
如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=-2x+1交于点A(-1,a)(1)求a,m的值;
(2)点P是双曲线y=$\frac{m}{x}$上的一点,且OP与直线y=-2x+1平行,求点P的横坐标.
分析 (1)根据双曲线y=$\frac{m}{x}$与直线y=-2x+1交于点A(-1,a),将点A的横纵坐标代入y=-2x+1中可以求得a的值,然后再代入反比例函数解析式中即可求得m的值;
(2)根据OP与直线y=-2x+1平行,可以直接得到直线OP的解析式,再根据点P是双曲线y=$\frac{m}{x}$上的一点,即可求得点P的横坐标.
解答 解:(1)∵双曲线y=$\frac{m}{x}$与直线y=-2x+1交于点A(-1,a),
∴将x=-1代入y=-2x+1,得
y=-2×(-1)+1=2+1=3,
∴点A(-1,3)
∴a=3,
∵点A(-1,3)在双曲线y=$\frac{m}{x}$上,
∴3=$\frac{m}{-1}$,得m=-3,
即a的值是3,m的值是-3;
(2)∵OP与直线y=-2x+1平行,
∴直线OP的解析式为y=-2x,
∵点P在双曲线y=$\frac{m}{x}$上,
∴-2x=$\frac{-3}{x}$,
解得,x=$±\frac{\sqrt{6}}{2}$,
即点P的横坐标是$\frac{\sqrt{6}}{2}$或$-\frac{\sqrt{6}}{2}$.
点评 本题考查反比例函数与一次函数的交点问题,解答本题的关键是明确题意,找出所求问题需要的条件,利用反比例函数的性质解答.

练习册系列答案
相关题目
13.若分式$\frac{2}{x-1}$有意义,则x的取值范围是( )
| A. | x=1 | B. | x≠1 | C. | x>1 | D. | x<1 |
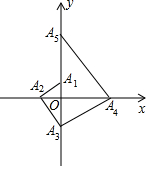 如图,点A1的坐标为(0,1),A2在x轴的负半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交y轴于点A3;过点A3作A3A4⊥A2A3,垂足为A3,交x轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交y轴于点A5;…按此规律进行下去,则点A2017的坐标为(0,31008).
如图,点A1的坐标为(0,1),A2在x轴的负半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交y轴于点A3;过点A3作A3A4⊥A2A3,垂足为A3,交x轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交y轴于点A5;…按此规律进行下去,则点A2017的坐标为(0,31008).
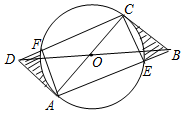 已知:如图,AC是⊙O的直径,圆心为点O,过A,C两点分别作⊙的切线,过圆心O的直线分别交这两条切线于B,D.
已知:如图,AC是⊙O的直径,圆心为点O,过A,C两点分别作⊙的切线,过圆心O的直线分别交这两条切线于B,D.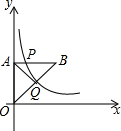 如图,平面直角坐标系中,O为坐标原点,等腰Rt△OAB的顶点B在第一象限,直角边OA在y轴上,点P是边AB上的一个三等分点,过点P的反比例函数y=$\frac{k}{x}$的图象交斜边OB于点Q,△AOQ的面积为3,则k的值为2$\sqrt{3}$或2$\sqrt{6}$.
如图,平面直角坐标系中,O为坐标原点,等腰Rt△OAB的顶点B在第一象限,直角边OA在y轴上,点P是边AB上的一个三等分点,过点P的反比例函数y=$\frac{k}{x}$的图象交斜边OB于点Q,△AOQ的面积为3,则k的值为2$\sqrt{3}$或2$\sqrt{6}$.