题目内容
12.已知关于x的一元二次方程:k2x2+(1-2k)x+1=0有两个不相等的实数根.(1)求k的取值范围;
(2)若原方程的两个实数根为x1、x2,且满足|x1|+|x2|=2x1x2-3,求k的值.
分析 (1)根据一元二次方程的定义和判别式的意义得到∴△=(1-2k)2-4k2>0且k2≠0,然后求出两个不等式的公共部分即可;
(2)利用根与系数的关系得到x1+x2=$\frac{2k-1}{{k}^{2}}$,x1x2=$\frac{1}{{k}^{2}}$,加上k<$\frac{1}{4}$且k≠0,则可判断x1<0,x2<0,所以-x1-x2=2x1x2-3,即-(x1+x2)=2x1x2-3.则$-\frac{2k-1}{k^2}=\frac{2}{k^2}-3$,然后解方程求出k即可得到满足条件的k的值.
解答 解:(1)∵关于x的一元二次方程k2x2+(1-2k)x+1=0有两个不相等的实数根,
∴△=(1-2k)2-4k2>0且k2≠0,
解得k<$\frac{1}{4}$且k≠0,
∴k的取值范围是k<$\frac{1}{4}$且k≠0;
(2)∵原方程的两个实数根为x1、x2,
∴x1+x2=$\frac{2k-1}{{k}^{2}}$,x1x2=$\frac{1}{{k}^{2}}$,
而k<$\frac{1}{4}$且k≠0;
∴x1+x2=$\frac{2k-1}{{k}^{2}}$<0,x1x2=$\frac{1}{{k}^{2}}$>0,
∴x1<0,x2<0,
∵|x1|+|x2|=2x1x2-3,
∴-x1-x2=2x1x2-3,即-(x1+x2)=2x1x2-3.
∴$-\frac{2k-1}{k^2}=\frac{2}{k^2}-3$,
整理得 3k2-2k-1=0,
解得:k1=1,${k_2}=-\frac{1}{3}$.
又∵$k<\frac{1}{4}$且k≠0,
∴k1=1不合题意,舍去.
经检验,${k_2}=-\frac{1}{3}$是方程$-\frac{2k-1}{k^2}=\frac{2}{k^2}-3$的解.
∴k的值为$-\frac{1}{3}$.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了根的判别式.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案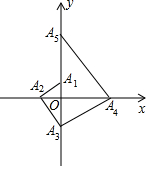 如图,点A1的坐标为(0,1),A2在x轴的负半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交y轴于点A3;过点A3作A3A4⊥A2A3,垂足为A3,交x轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交y轴于点A5;…按此规律进行下去,则点A2017的坐标为(0,31008).
如图,点A1的坐标为(0,1),A2在x轴的负半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交y轴于点A3;过点A3作A3A4⊥A2A3,垂足为A3,交x轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交y轴于点A5;…按此规律进行下去,则点A2017的坐标为(0,31008).
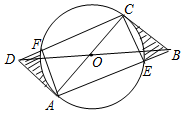 已知:如图,AC是⊙O的直径,圆心为点O,过A,C两点分别作⊙的切线,过圆心O的直线分别交这两条切线于B,D.
已知:如图,AC是⊙O的直径,圆心为点O,过A,C两点分别作⊙的切线,过圆心O的直线分别交这两条切线于B,D.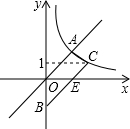 如图,梯形AOBC的顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x上,下底边BC交y轴于B(0,-4),则四边形AOBC的面积为2$\sqrt{5}$+10.
如图,梯形AOBC的顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x上,下底边BC交y轴于B(0,-4),则四边形AOBC的面积为2$\sqrt{5}$+10. 阅读下面材料:
阅读下面材料: