题目内容
18．
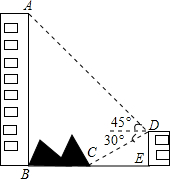如图，大楼AB右侧有一障碍物，在障碍物的旁边有一幢小楼DE，在小楼的顶端D处测得障碍物边缘点C的俯角为30°，测得大楼顶端A的仰角为45°（点B，C，E在同一水平直线上），已知AB=60m，DE=10m，求障碍物B，C两点间的距离（结果精确到0.1m）（参考数据：$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732）
分析 如图，过点D作DF⊥AB于点F，过点C作CH⊥DF于点H．在Rt△ADF中，求出DF，在Rt△CDE中，求出CE即可．
解答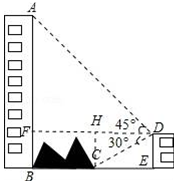 
解：如图，过点D作DF⊥AB于点F，过点C作CH⊥DF于点H．
则DE=BF=CH=10m，
在直角△ADF中，∵AF=60m-10m=50m，∠ADF=45°，
∴DF=AF=50m．
在直角△CDE中，∵DE=10m，∠DCE=30°，
∴CE=$\frac{DE}{tan30°}$=$\frac{10}{\frac{\sqrt{3}}{3}}$=10$\sqrt{3}$（m），
∴BC=BE-CE=50-10$\sqrt{3}$≈50-17.32≈32.7（m）．
答：障碍物B，C两点间的距离约为32.7m．
点评 本题考查解直角三角形的应用-仰角俯角问题，锐角三角函数等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考常考题型．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
新思维寒假作业系列答案
相关题目
15．方程$\frac{2}{x+3}$=$\frac{1}{x-1}$的解是（ ）
| A． | x=$\frac{5}{3}$ | B． | x=5 | C． | x=4 | D． | x=-5 |
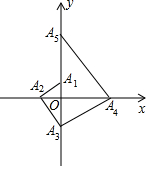如图，点A1的坐标为（0，1），A2在x轴的负半轴上，且∠A1A2O=30°，过点A2作A2A3⊥A1A2，垂足为A2，交y轴于点A3；过点A3作A3A4⊥A2A3，垂足为A3，交x轴于点A4；过点A4作A4A5⊥A3A4，垂足为A4，交y轴于点A5；…按此规律进行下去，则点A2017的坐标为（0，31008）．
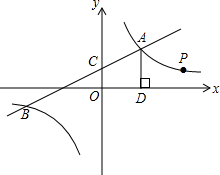如图，一次函数y1=k1x+b与反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于点A（4，m）和B（-8，-2），与y轴交于点C．