题目内容
课堂上,老师提出这样一个问题:你能用手中的矩形纸片尽可能大的折出一个菱形吗?有两位同学很快折出了各自不同的菱形,如下图:
(1)如果该矩形纸片的长为4,宽为3,则图1、图2两图中的菱形面积分别为: ; ;
(2)这时老师说,这两位同学折出的菱形都不是最大的,聪明的你能够想出最大的菱形应该怎样折出来吗?如图3所示:在矩形ABCD中,设AB=3,AD=4,请你在图中画出面积最大的菱形的示意图,标注上适当的字母,并求出这个菱形的面积.
(3)借题发挥:如图4,在矩形ABCD中,AB=2,AD=3,若折叠该矩形,使得点D与AB边的中点E重合,折痕交AD于点F,交BC于点G,边DC折叠后与BC交于点M,试求:△EBM的面积.
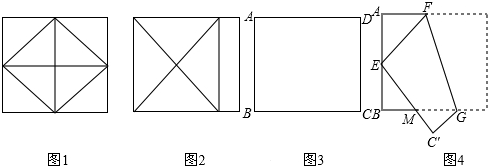
(1)如果该矩形纸片的长为4,宽为3,则图1、图2两图中的菱形面积分别为:
(2)这时老师说,这两位同学折出的菱形都不是最大的,聪明的你能够想出最大的菱形应该怎样折出来吗?如图3所示:在矩形ABCD中,设AB=3,AD=4,请你在图中画出面积最大的菱形的示意图,标注上适当的字母,并求出这个菱形的面积.
(3)借题发挥:如图4,在矩形ABCD中,AB=2,AD=3,若折叠该矩形,使得点D与AB边的中点E重合,折痕交AD于点F,交BC于点G,边DC折叠后与BC交于点M,试求:△EBM的面积.

考点:几何变换综合题
专题:
分析:1)由菱形的面积等于两条对角线的积的一半和正方形的面积公式计算;
(2)以BD为对角线,E、F分别在AD,BC上,且EF垂直平分BD,在Rt△ABE中,由勾股定理可求得BE的长,即为DE的长,则S菱形EAFD=DE•AB;
(3)由于AE=BE=1,则在Rt△AEF中,根据勾股定理可求得AF的值,由角的关系可求得△AEF∽△BME,则
=
,求得BM的长,则S△EBM=
BE•BM.
(2)以BD为对角线,E、F分别在AD,BC上,且EF垂直平分BD,在Rt△ABE中,由勾股定理可求得BE的长,即为DE的长,则S菱形EAFD=DE•AB;
(3)由于AE=BE=1,则在Rt△AEF中,根据勾股定理可求得AF的值,由角的关系可求得△AEF∽△BME,则
| AF |
| BE |
| AE |
| BM |
| 1 |
| 2 |
解答: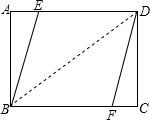 解:(1)第一个菱形的面积=3×4÷2=6,
解:(1)第一个菱形的面积=3×4÷2=6,
第二个菱形也是正方形,边长为3,则其面积=3×3=9.
故答案是:6,9;
(2)如图:(以BD或AC为对角线,E、F在AD,BC上,且EF垂直平分BD或AC).
解:如图设线段ED的长为x.
∵四边形BFDE是菱形∴ED=BE=x
又∵矩形ABCD中AB=3,AD=4
∴AE=4-x
在Rt△ABE中AE2+AB2=BE2
∴(4-x)2+32=x2
解之得:x=
,
∴ED=
.
∴S菱形EAFD=DE•AB=
;
(3)如图:
∵对折
∴DF=EF
设线段DF的长为x,则EF=x
∵AD=3
∴AF=3-x
∵点E是AB的中点,且AB=2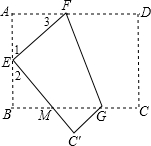
∴AE=BE=1
在Rt△AEF中有AE2+AF2=EF2
∴12+(3-x)2=x2
解之得:x=
∴AF=3-x=
,
在矩形ABCD中由于对折
∴∠D=∠FEM=90°∴∠1+∠2=90°
又∵∠A=∠B=90°
∴∠1+∠3=90°
∴∠2=∠3
∴△AEF∽△BME,
∴
=
,
∴BM=
.
∴S△EBM=
BE•BM=
.
 解:(1)第一个菱形的面积=3×4÷2=6,
解:(1)第一个菱形的面积=3×4÷2=6,第二个菱形也是正方形,边长为3,则其面积=3×3=9.
故答案是:6,9;
(2)如图:(以BD或AC为对角线,E、F在AD,BC上,且EF垂直平分BD或AC).
解:如图设线段ED的长为x.
∵四边形BFDE是菱形∴ED=BE=x
又∵矩形ABCD中AB=3,AD=4
∴AE=4-x
在Rt△ABE中AE2+AB2=BE2
∴(4-x)2+32=x2
解之得:x=
| 25 |
| 8 |
∴ED=
| 25 |
| 8 |
∴S菱形EAFD=DE•AB=
| 75 |
| 8 |
(3)如图:
∵对折
∴DF=EF
设线段DF的长为x,则EF=x
∵AD=3
∴AF=3-x
∵点E是AB的中点,且AB=2

∴AE=BE=1
在Rt△AEF中有AE2+AF2=EF2
∴12+(3-x)2=x2
解之得:x=
| 5 |
| 3 |
∴AF=3-x=
| 4 |
| 3 |
在矩形ABCD中由于对折
∴∠D=∠FEM=90°∴∠1+∠2=90°
又∵∠A=∠B=90°
∴∠1+∠3=90°
∴∠2=∠3
∴△AEF∽△BME,
∴
| AF |
| BE |
| AE |
| BM |
∴BM=
| 3 |
| 4 |
∴S△EBM=
| 1 |
| 2 |
| 3 |
| 8 |
点评:本题考查了翻折的性质:对应角相等,对应边相等,以及菱形和正方形、矩形的性质和勾股定理.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
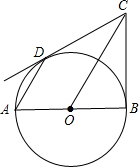 如图,已知AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD.
如图,已知AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD.(1)求证:DC是⊙O的切线;
(2)若OB=1,劣弧
 |
| BD |
已知等腰三角形的两边长分别为6和5,则这个等腰三角形的周长是( )
| A、15或16 | B、16 |
| C、17 | D、16或17 |
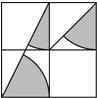 如图,方格纸中4个小正方形的边长均为1,求图中阴影部分三个小扇形的面积和以及周长的和(结果保留π).
如图,方格纸中4个小正方形的边长均为1,求图中阴影部分三个小扇形的面积和以及周长的和(结果保留π).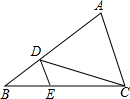 如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△DEC:S△ADC=1:3,则S△BDE:S△ACD=
如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△DEC:S△ADC=1:3,则S△BDE:S△ACD=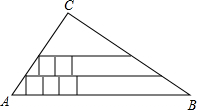 如图,在Rt△ABC中,∠C为直角,AC=6,BC=8.在Rt△ABC内从左往右叠放边长为1.2的正方形小纸片,第一层小纸片的一条边都在AB上,依次这样往上叠放上去,则最多能叠放
如图,在Rt△ABC中,∠C为直角,AC=6,BC=8.在Rt△ABC内从左往右叠放边长为1.2的正方形小纸片,第一层小纸片的一条边都在AB上,依次这样往上叠放上去,则最多能叠放 如图,图中同位角一共
如图,图中同位角一共