题目内容
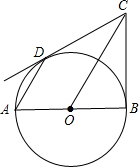 如图,已知AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD.
如图,已知AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD.(1)求证:DC是⊙O的切线;
(2)若OB=1,劣弧
 |
| BD |
考点:切线的判定,扇形面积的计算
专题:
分析:(1)如图,作辅助线;证明△COD≌△COB,得到∠CDO=∠CBO;证明∠CBO=90°,即可解决问题.
(2)直接运用扇形面积的计算公式计算,即可解决问题.
(2)直接运用扇形面积的计算公式计算,即可解决问题.
解答: (1)证明:如图,连接OD;
(1)证明:如图,连接OD;
∵OC∥AD,
∴∠OAD=∠BOC,∠ODA=∠COD;而OA=OD,
∴∠OAD=∠ODA,∠COD=∠BOC;
在△COD与△COB中,
,
∴△COD≌△COB(SAS),
∴∠CDO=∠CBO;
∵BC是⊙O的切线,
∴∠CBO=90°,
∴∠CDO=90°,即DC是⊙O的切线.
(2)解:S扇形BOD=
=
.
 (1)证明:如图,连接OD;
(1)证明:如图,连接OD;∵OC∥AD,
∴∠OAD=∠BOC,∠ODA=∠COD;而OA=OD,
∴∠OAD=∠ODA,∠COD=∠BOC;
在△COD与△COB中,
|
∴△COD≌△COB(SAS),
∴∠CDO=∠CBO;
∵BC是⊙O的切线,
∴∠CBO=90°,
∴∠CDO=90°,即DC是⊙O的切线.
(2)解:S扇形BOD=
| 130π×12 |
| 360 |
| 13π |
| 36 |
点评:该题主要考查了圆的切线的判定、扇形面积的计算等几何知识点及其应用问题;解题的关键是准确判断切线的判定方法;灵活运用切线的判定、扇形面积的计算来分析、解答.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
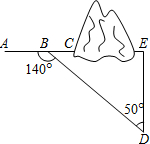 如图,沿AC方向开山修路,为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B取∠ABD=140°,BD=520m,∠D=50°,那么另一边开挖点E离D多远正好使A,C,E三点在一直线上(结果保留小数点后一位)?
如图,沿AC方向开山修路,为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B取∠ABD=140°,BD=520m,∠D=50°,那么另一边开挖点E离D多远正好使A,C,E三点在一直线上(结果保留小数点后一位)?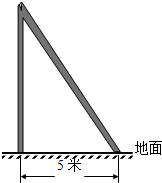 如图,一木杆原来垂直于地面,在离地某处断裂,木杆顶部落在离木杆底部5米处,已知木杆原长25米,求木杆断裂处离地面多少米?
如图,一木杆原来垂直于地面,在离地某处断裂,木杆顶部落在离木杆底部5米处,已知木杆原长25米,求木杆断裂处离地面多少米?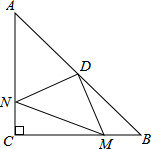 在△ABC中,∠ACB=90°,AC=BC=4,点D为AB的中点,M、N分别在BC、AC上,且BM=CN.
在△ABC中,∠ACB=90°,AC=BC=4,点D为AB的中点,M、N分别在BC、AC上,且BM=CN.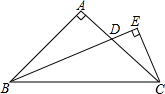 如图,在Rt△ABC中,AB=AC,∠BAC=90°,BD平分∠ABC交AC于点D,CE⊥BD交BD的延长线于点E,则线段BD和CE具有什么数量关系,并证明你的结论.
如图,在Rt△ABC中,AB=AC,∠BAC=90°,BD平分∠ABC交AC于点D,CE⊥BD交BD的延长线于点E,则线段BD和CE具有什么数量关系,并证明你的结论.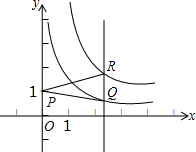 函数y=
函数y=