题目内容
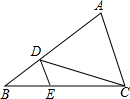 如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△DEC:S△ADC=1:3,则S△BDE:S△ACD=
如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△DEC:S△ADC=1:3,则S△BDE:S△ACD=考点:相似三角形的判定与性质
专题:
分析:如图,作辅助线;证明
=
=
,得到
=
;证明△BDE∽△ABC,得到S△ABC=9S△BDE,由S△ABC=4λ+S△BDE,求得S△BDE=0.5λ,即可解决问题.
| S△DEC |
| S△ADC |
| ||
|
| DE |
| AC |
| DE |
| AC |
| 1 |
| 3 |
解答: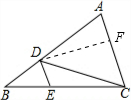 解:过点D作DF⊥AC于点F;
解:过点D作DF⊥AC于点F;
∵DE∥AC,
∴DF为△ADC、△DEC的公共高,
∴
=
=
,
∵S△DEC:S△ADC=1:3,
∴DE:AC=1:3;若设S△DEC=λ,则S△ADC=3λ;
∵DE∥AC,
∴△BDE∽△ABC,
∴
=(
)2=
,
∴S△ABC=9S△BDE,而S△ABC=4λ+S△BDE,
∴S△BDE=0.5λ,
∴S△BDE:S△ACD=1:6,
故答案为1:6.
 解:过点D作DF⊥AC于点F;
解:过点D作DF⊥AC于点F;∵DE∥AC,
∴DF为△ADC、△DEC的公共高,
∴
| S△DEC |
| S△ADC |
| ||
|
| DE |
| AC |
∵S△DEC:S△ADC=1:3,
∴DE:AC=1:3;若设S△DEC=λ,则S△ADC=3λ;
∵DE∥AC,
∴△BDE∽△ABC,
∴
| S△BDE |
| S△ABC |
| DE |
| AC |
| 1 |
| 9 |
∴S△ABC=9S△BDE,而S△ABC=4λ+S△BDE,
∴S△BDE=0.5λ,
∴S△BDE:S△ACD=1:6,
故答案为1:6.
点评:该题主要考查了相似三角形的判定及其性质、三角形的面积公式等几何知识点及其应用问题;解题的关键是灵活运用相似三角形的判定及其性质、三角形的面积公式等来分析、判断、解答.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
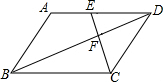 如图,在平行四边形ABCD中,点E是边AD上的一点,且AE:ED=2:3,EC交对角线BD于点F,则EF:FC等于( )
如图,在平行四边形ABCD中,点E是边AD上的一点,且AE:ED=2:3,EC交对角线BD于点F,则EF:FC等于( )| A、3:2 | B、2:5 |
| C、2:3 | D、3:5 |
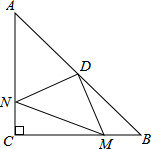 在△ABC中,∠ACB=90°,AC=BC=4,点D为AB的中点,M、N分别在BC、AC上,且BM=CN.
在△ABC中,∠ACB=90°,AC=BC=4,点D为AB的中点,M、N分别在BC、AC上,且BM=CN.
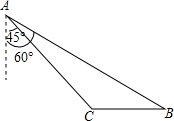 如图,到海岛景区C有两条旅游线路可供选择,游人可从码头A乘游艇或从码头B乘游船前往,已知B在A南偏东60°方向,C位于A南偏东45°方向10海里处,且C在B正西方向,游艇的速度为每小时30海里,游船的速度为每小时13海里,问游客选择哪条线路用时较少?并说明理由.(参考数据:
如图,到海岛景区C有两条旅游线路可供选择,游人可从码头A乘游艇或从码头B乘游船前往,已知B在A南偏东60°方向,C位于A南偏东45°方向10海里处,且C在B正西方向,游艇的速度为每小时30海里,游船的速度为每小时13海里,问游客选择哪条线路用时较少?并说明理由.(参考数据: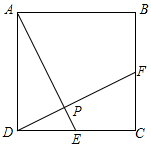 正方形ABCD中,E,F分别为边DC,BC上的点,连接AE,DF且AE⊥DF于点P.
正方形ABCD中,E,F分别为边DC,BC上的点,连接AE,DF且AE⊥DF于点P.
 如图,已知∠AOB=∠COD=90°,又∠AOD=170°,则∠BOC=
如图,已知∠AOB=∠COD=90°,又∠AOD=170°,则∠BOC=