题目内容
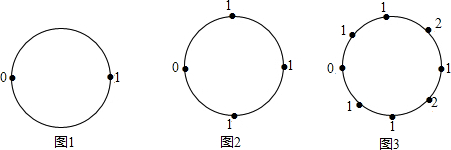
如图所示,每个圆周上的数是按下述规则逐次标出的:第一次先在圆周上标出0,1两个数(如图1);第二次又在第一次标出的两个数之间的圆周上,分别标出这两个数的和(图2);第三次再在第二次标出的所有相邻两数之间的圆周上,分别标出相邻两数的和(如图3).按此规则以此类推,第2013次标完数字后,圆周上所有数字的和S2013= .

考点:规律型:数字的变化类
专题:
分析:当n=1时,S=1;当n=2时,S=3;当n=3时,S=9;当n=4时,S=27;由此可知每一次标完后的都是3的n-1次方,即可推出Sn.
解答:解:∵当n=1时,S=1;
当n=2时,S=3;
当n=3时,S=9;
当n=4时,S=27;
…
∴Sn=3n-1;
∴S2013=32012.
故答案为:32012.
当n=2时,S=3;
当n=3时,S=9;
当n=4时,S=27;
…
∴Sn=3n-1;
∴S2013=32012.
故答案为:32012.
点评:此题考查数字的变化规律,找出数字之间的运算规律,利用规律解决问题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
甲、乙两人都去同一家超市购买大米各两次,甲每次购买50千克的大米,乙每次够买50元的大米,这两人第一次够买大米时售价为每千克m元,第二次够买大米时售价为每千克n元(m≠n),若规定谁两次够买大米的平均单价低,谁的够买方式就合算,则( )
| A、甲的够买方式合算 |
| B、乙的够买方式合算 |
| C、甲、乙的够买方式同样合算 |
| D、不能判断谁的够买方式合算 |
顶点坐标为(-2,3),开口方向和大小与抛物线y=x2相同的解析式为( )
| A、y=(x-2)2+3 |
| B、y=(x+2)2-3 |
| C、y=(x+2)2+3 |
| D、y=-(x+2)2+3 |
 如图,已知∠AOB=∠COD=90°,又∠AOD=170°,则∠BOC=
如图,已知∠AOB=∠COD=90°,又∠AOD=170°,则∠BOC=