题目内容
17.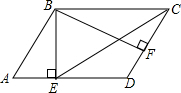 在平行四边形ABCD中,BE⊥AD于点E,BF⊥CD于点F,若∠EBF=60°,且AE=2,DF=1,则EC的长为4$\sqrt{3}$.
在平行四边形ABCD中,BE⊥AD于点E,BF⊥CD于点F,若∠EBF=60°,且AE=2,DF=1,则EC的长为4$\sqrt{3}$.
分析 由平行四边形的性质和已知条件得出∠ABE=∠CBF=30°,得出CD=AB=2AE=4,由勾股定理求出BE,得出BC=2CF=6,再根据勾股定理即可求出EC.
解答 解:∵四边形ABCD是平行四边形,
∴AB∥CD,BC∥AD,AB=CD,
∵BE⊥AD,BF⊥CD,
∴BE⊥BC,BF⊥AB,
∴∠ABF=∠EBC=90°,
∵∠EBF=60°,
∴∠ABE=∠CBF=30°,
∵AE=2,DF=1,
∴CD=AB=2AE=4,
∴BE=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,CF=4-1=3,
∴BC=2CF=6,
∴EC=$\sqrt{B{C}^{2}+B{E}^{2}}$=$\sqrt{{6}^{2}+(2\sqrt{3})^{2}}$=4$\sqrt{3}$;
故答案为:4$\sqrt{3}$.
点评 本题考查了平行四边形的性质、勾股定理、含30°角的直角三角形的性质;熟练掌握平行四边形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
5.已知A组有三个数:1,-2,3,B组有三个数:1,-$\sqrt{2}$,$\sqrt{3}$,若从B组任选两个数分别与A组的每个数相乘,共得到6个数,再把这6个数相加得到数m,则m>0的概率为( )
| A. | 0 | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | 1 |
3.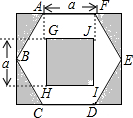 如图,某小区为增加居民的活动面积,将一块矩形空地设计为休闲区域,其中正六边形ABCDEF的顶点均在矩形边上,正六边形内部有一正方形GHIJ.根据设计,图中阴影部分种植草坪,则草坪面积为( )
如图,某小区为增加居民的活动面积,将一块矩形空地设计为休闲区域,其中正六边形ABCDEF的顶点均在矩形边上,正六边形内部有一正方形GHIJ.根据设计,图中阴影部分种植草坪,则草坪面积为( )
 如图,某小区为增加居民的活动面积,将一块矩形空地设计为休闲区域,其中正六边形ABCDEF的顶点均在矩形边上,正六边形内部有一正方形GHIJ.根据设计,图中阴影部分种植草坪,则草坪面积为( )
如图,某小区为增加居民的活动面积,将一块矩形空地设计为休闲区域,其中正六边形ABCDEF的顶点均在矩形边上,正六边形内部有一正方形GHIJ.根据设计,图中阴影部分种植草坪,则草坪面积为( )| A. | a2 | B. | ($\frac{\sqrt{3}}{2}$+1)a2 | C. | 2a2 | D. | $\frac{\sqrt{3}+1}{2}$a2 |
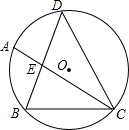 如图,△DBC内接于⊙O,DB=DC,$\widehat{AB}$=$\widehat{BC}$,DB交AC于E.
如图,△DBC内接于⊙O,DB=DC,$\widehat{AB}$=$\widehat{BC}$,DB交AC于E.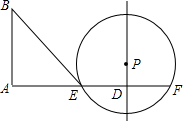 如图,已知线段AD=10,过点D作PD⊥AD于D,点P是直线PD上一点,且PD=3,以点P为圆心,半径为5作⊙P交线段AD于点E及AD的延长线于点F,又过点A作BA⊥AD于A,BA=8,连接BE、PE.
如图,已知线段AD=10,过点D作PD⊥AD于D,点P是直线PD上一点,且PD=3,以点P为圆心,半径为5作⊙P交线段AD于点E及AD的延长线于点F,又过点A作BA⊥AD于A,BA=8,连接BE、PE.