题目内容
3.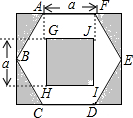 如图,某小区为增加居民的活动面积,将一块矩形空地设计为休闲区域,其中正六边形ABCDEF的顶点均在矩形边上,正六边形内部有一正方形GHIJ.根据设计,图中阴影部分种植草坪,则草坪面积为( )
如图,某小区为增加居民的活动面积,将一块矩形空地设计为休闲区域,其中正六边形ABCDEF的顶点均在矩形边上,正六边形内部有一正方形GHIJ.根据设计,图中阴影部分种植草坪,则草坪面积为( )| A. | a2 | B. | ($\frac{\sqrt{3}}{2}$+1)a2 | C. | 2a2 | D. | $\frac{\sqrt{3}+1}{2}$a2 |
分析 首先根据正六边形的性质求得∠MAB的度数,然后求得三角形MAB的面积,用4个三角形的面积加上正方形的面积即可求得阴影部分的面积.
解答  解:如图:∵六边形ABCDEF是正六边形,
解:如图:∵六边形ABCDEF是正六边形,
∴∠BAF=120°,AF=AB=a,
∴∠BAM=60°,
∴MA=$\frac{a}{2}$,MB=$\frac{\sqrt{3}}{2}$a,
∴S△ABM=$\frac{1}{2}$MA•MB=$\frac{1}{2}$×$\frac{a}{2}$×$\frac{\sqrt{3}}{2}$a=$\frac{\sqrt{3}}{8}$a2,
∴S阴影=4S△ABM+S正方形GHIJ=($\frac{\sqrt{3}}{2}$+1)a2,
故选B.
点评 本题考查了列代数式的知识,解题的关键是根据正六边形的性质求得三角形MAB的面积,难度不大.

练习册系列答案
相关题目
18.为了鼓励市民节约用水,盐城市居民生活用水按阶梯式水价计费.下表是盐城市居民“一户一表”生活用水阶梯式计费价格表的一部分信息:
(说明:①每户产生的污水量等于该户的用水量,②水费=自来水费+污水处理费)
已知小明家2015年2月份用水20吨,交水费66元;3月份用水35吨,交水费150元.
(1)求a、b的值.
(2)实行“阶梯水价”收费之后,该市一户居民用水多少吨时,其当月的平均水费为每吨3.3元?
| 用户每月用水量 | 自来水单价(元/吨) | 污水处理费用(元/吨) |
| 17吨及以下 | a | 0.80 |
| 超过17吨不超过30吨的部分 | b | 0.80 |
| 超过30吨的部分 | 6.00 | 0.80 |
已知小明家2015年2月份用水20吨,交水费66元;3月份用水35吨,交水费150元.
(1)求a、b的值.
(2)实行“阶梯水价”收费之后,该市一户居民用水多少吨时,其当月的平均水费为每吨3.3元?
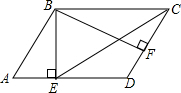 在平行四边形ABCD中,BE⊥AD于点E,BF⊥CD于点F,若∠EBF=60°,且AE=2,DF=1,则EC的长为4$\sqrt{3}$.
在平行四边形ABCD中,BE⊥AD于点E,BF⊥CD于点F,若∠EBF=60°,且AE=2,DF=1,则EC的长为4$\sqrt{3}$.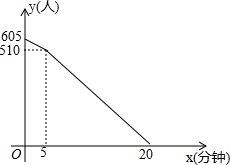 “五.一”假期,某火车客运站旅客流量明显增大,动车一般在开车前30分钟开始检票.假设某趟动车开始检票时已有605人到候车室排队检票,在检票开始5分钟内每分钟还有5个旅客进候车室进行检票,5分钟后到检票结束每分钟还会有2人到候车室排队检票,每分钟每个检票窗口检票12人(火车站会根据候车人数调研开放检票窗口数).此趟动车候车室排队等候检票的人数y(人)与检票时间x(分钟)的关系如图所示.根据关系图解答下列问题:
“五.一”假期,某火车客运站旅客流量明显增大,动车一般在开车前30分钟开始检票.假设某趟动车开始检票时已有605人到候车室排队检票,在检票开始5分钟内每分钟还有5个旅客进候车室进行检票,5分钟后到检票结束每分钟还会有2人到候车室排队检票,每分钟每个检票窗口检票12人(火车站会根据候车人数调研开放检票窗口数).此趟动车候车室排队等候检票的人数y(人)与检票时间x(分钟)的关系如图所示.根据关系图解答下列问题: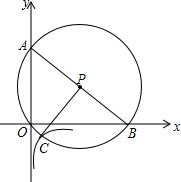 如图,在平面直角坐标系中,经过原点的圆P交坐标轴于点A,B,过点P作AB的垂线交圆P于点C,反比例函数y=$\frac{k}{x}$的图象经过点C.若OB-OA=4,则k的值为-4.
如图,在平面直角坐标系中,经过原点的圆P交坐标轴于点A,B,过点P作AB的垂线交圆P于点C,反比例函数y=$\frac{k}{x}$的图象经过点C.若OB-OA=4,则k的值为-4.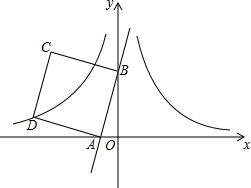 如图,在平面直角坐标系中,直线y=3x+3与x轴、y轴分别交于A、B两点,以AB为边在第二象限作正方形ABCD.将过D点的双曲线y=$\frac{{k}_{1}}{x}$(x<0)沿y轴对折,得到双曲线y=$\frac{{k}_{2}}{x}$(x>0),将正方形ABCD沿x轴正方向向右平移a个单位长度后,点C恰好也落在此双曲线y=$\frac{{k}_{2}}{x}$(x>0)上,则a的值是( )
如图,在平面直角坐标系中,直线y=3x+3与x轴、y轴分别交于A、B两点,以AB为边在第二象限作正方形ABCD.将过D点的双曲线y=$\frac{{k}_{1}}{x}$(x<0)沿y轴对折,得到双曲线y=$\frac{{k}_{2}}{x}$(x>0),将正方形ABCD沿x轴正方向向右平移a个单位长度后,点C恰好也落在此双曲线y=$\frac{{k}_{2}}{x}$(x>0)上,则a的值是( )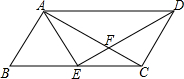 如图,E是?ABCD的边BC的中点,AC⊥AB,∠B=60°.则下列结论中正确的是①②④.(把所有正确结论的序号都填在横线上)
如图,E是?ABCD的边BC的中点,AC⊥AB,∠B=60°.则下列结论中正确的是①②④.(把所有正确结论的序号都填在横线上)