题目内容
6.解方程组:(1)$\left\{\begin{array}{l}{x-5y-3z=-4}\\{3x+5y+z=-2}\\{x-3y-5z=-6}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{\frac{x}{4}=\frac{y}{5}=\frac{z}{6}}\\{2x+3y-4z+3=0}\end{array}\right.$.
分析 (1)根据加减消元消去x,然后利用二元一次方程组解法解答即可;
(2)先把$\frac{x}{4}=\frac{y}{5}=\frac{z}{6}=k$,得出x=4k,y=5k,z=6k再代入解答即可.
解答 解:(1)$\left\{\begin{array}{l}{x-5y-3z=-4①}\\{3x+5y+z=-2②}\\{x-3y-5z=-6③}\end{array}\right.$,
③-①得:y-z=-1④,
②-③×3得:7y+8z=8⑤,
把④代入⑤得:z=1,
把z=1代入④得:y=0,
把z=1,y=0代入①得:x=-1,
所以方程组的解是:$\left\{\begin{array}{l}{x=-1}\\{y=0}\\{z=1}\end{array}\right.$;
(2)把①变形为:$\frac{x}{4}=\frac{y}{5}=\frac{z}{6}=k$,
可得:x=4k,y=5k,z=6k,
把x=4k,y=5k,z=6k代入②得:8k+15k-24k+3=0,
解得:k=3,
所以x=4k=12,y=5k=15,z=6k=18,
所以方程组的解是:$\left\{\begin{array}{l}{x=12}\\{y=15}\\{z=18}\end{array}\right.$.
点评 此题考查方程组的解法,关键是代入消元和加减消元法的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
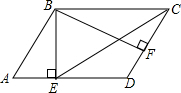 在平行四边形ABCD中,BE⊥AD于点E,BF⊥CD于点F,若∠EBF=60°,且AE=2,DF=1,则EC的长为4$\sqrt{3}$.
在平行四边形ABCD中,BE⊥AD于点E,BF⊥CD于点F,若∠EBF=60°,且AE=2,DF=1,则EC的长为4$\sqrt{3}$.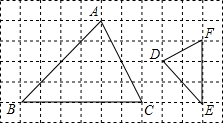 △ABC与△DEF在网格中的位置如图所示,如果每个小正方形的边长都是1.
△ABC与△DEF在网格中的位置如图所示,如果每个小正方形的边长都是1. 如图所示,用不等式表示零件长度的合格尺寸的取值范围是39.8≤L≤40.2.
如图所示,用不等式表示零件长度的合格尺寸的取值范围是39.8≤L≤40.2.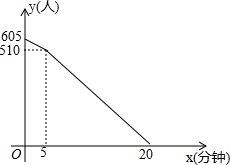 “五.一”假期,某火车客运站旅客流量明显增大,动车一般在开车前30分钟开始检票.假设某趟动车开始检票时已有605人到候车室排队检票,在检票开始5分钟内每分钟还有5个旅客进候车室进行检票,5分钟后到检票结束每分钟还会有2人到候车室排队检票,每分钟每个检票窗口检票12人(火车站会根据候车人数调研开放检票窗口数).此趟动车候车室排队等候检票的人数y(人)与检票时间x(分钟)的关系如图所示.根据关系图解答下列问题:
“五.一”假期,某火车客运站旅客流量明显增大,动车一般在开车前30分钟开始检票.假设某趟动车开始检票时已有605人到候车室排队检票,在检票开始5分钟内每分钟还有5个旅客进候车室进行检票,5分钟后到检票结束每分钟还会有2人到候车室排队检票,每分钟每个检票窗口检票12人(火车站会根据候车人数调研开放检票窗口数).此趟动车候车室排队等候检票的人数y(人)与检票时间x(分钟)的关系如图所示.根据关系图解答下列问题: