题目内容
12.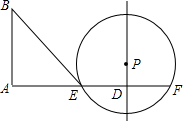 如图,已知线段AD=10,过点D作PD⊥AD于D,点P是直线PD上一点,且PD=3,以点P为圆心,半径为5作⊙P交线段AD于点E及AD的延长线于点F,又过点A作BA⊥AD于A,BA=8,连接BE、PE.
如图,已知线段AD=10,过点D作PD⊥AD于D,点P是直线PD上一点,且PD=3,以点P为圆心,半径为5作⊙P交线段AD于点E及AD的延长线于点F,又过点A作BA⊥AD于A,BA=8,连接BE、PE.(1)求线段EF的长;
(2)试判断直线BE与⊙P的位置关系,并说明你的理由.
分析 (1)根据垂径定理得出ED=DF=$\frac{1}{2}$EF,根据勾股定理得出ED=4,即可求得EF;
(2)先证得△BAE∽△PDE,从而求得∠ABE=∠PED,进而证得∠PEB=90°,即PE⊥BE,即可证得直线BE与⊙P相切.
解答 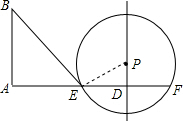 解:(1)∵PD⊥AD,点P为圆心,
解:(1)∵PD⊥AD,点P为圆心,
∴ED=DF=$\frac{1}{2}$EF,
连接PE,
在RT△PDE中,ED=$\sqrt{P{E}^{2}-P{D}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴EF=2ED=8;
(2)直线BE与⊙P相切;
∵AD=10,ED=4,
∴AE=10-4=6,
∵$\frac{BA}{AE}$=$\frac{8}{6}$=$\frac{4}{3}$,$\frac{ED}{PD}$=$\frac{4}{3}$,
∴$\frac{BA}{AE}$=$\frac{ED}{PD}$,
∵∠BAE=∠PDE=90°,
∴△BAE∽△PDE,
∴∠ABE=∠PED,
∵∠ABE+∠AEB=90°,
∴∠PED+∠AEB=90°,
∴∠PEB=90°,即PE⊥BE,
∴BE是⊙P的切线.
点评 此题考查了切线的判定,勾股定理,相似三角形的判定与性质,熟练掌握切线的判定是解本题的关键.

练习册系列答案
相关题目
18.为了鼓励市民节约用水,盐城市居民生活用水按阶梯式水价计费.下表是盐城市居民“一户一表”生活用水阶梯式计费价格表的一部分信息:
(说明:①每户产生的污水量等于该户的用水量,②水费=自来水费+污水处理费)
已知小明家2015年2月份用水20吨,交水费66元;3月份用水35吨,交水费150元.
(1)求a、b的值.
(2)实行“阶梯水价”收费之后,该市一户居民用水多少吨时,其当月的平均水费为每吨3.3元?
| 用户每月用水量 | 自来水单价(元/吨) | 污水处理费用(元/吨) |
| 17吨及以下 | a | 0.80 |
| 超过17吨不超过30吨的部分 | b | 0.80 |
| 超过30吨的部分 | 6.00 | 0.80 |
已知小明家2015年2月份用水20吨,交水费66元;3月份用水35吨,交水费150元.
(1)求a、b的值.
(2)实行“阶梯水价”收费之后,该市一户居民用水多少吨时,其当月的平均水费为每吨3.3元?
 如图,小华画出了一次函数y=-3x-3的图象的一部分,根据图象解答下面的问题:
如图,小华画出了一次函数y=-3x-3的图象的一部分,根据图象解答下面的问题: 如图,点P在平行四边形ABCD内,且∠ABP=∠ADP,求证:∠DAP=∠DCP.
如图,点P在平行四边形ABCD内,且∠ABP=∠ADP,求证:∠DAP=∠DCP.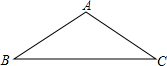 在等腰三角形中,过其中的一个顶点的直线如果能把这个等腰三角形分成两个小的等腰三角形,我们称这种等腰三角形为“少见的三角形”,这条直线称为分割线,下面我们来研究这类三角形.
在等腰三角形中,过其中的一个顶点的直线如果能把这个等腰三角形分成两个小的等腰三角形,我们称这种等腰三角形为“少见的三角形”,这条直线称为分割线,下面我们来研究这类三角形.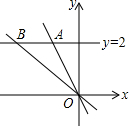 如图,直线y=2分别交正比例函数y=-2x,y=-$\frac{1}{2}$x的图象于A,B两点,求S△AOB.
如图,直线y=2分别交正比例函数y=-2x,y=-$\frac{1}{2}$x的图象于A,B两点,求S△AOB.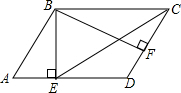 在平行四边形ABCD中,BE⊥AD于点E,BF⊥CD于点F,若∠EBF=60°,且AE=2,DF=1,则EC的长为4$\sqrt{3}$.
在平行四边形ABCD中,BE⊥AD于点E,BF⊥CD于点F,若∠EBF=60°,且AE=2,DF=1,则EC的长为4$\sqrt{3}$.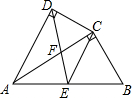 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点. 如图所示,用不等式表示零件长度的合格尺寸的取值范围是39.8≤L≤40.2.
如图所示,用不等式表示零件长度的合格尺寸的取值范围是39.8≤L≤40.2.