题目内容
8.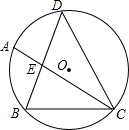 如图,△DBC内接于⊙O,DB=DC,$\widehat{AB}$=$\widehat{BC}$,DB交AC于E.
如图,△DBC内接于⊙O,DB=DC,$\widehat{AB}$=$\widehat{BC}$,DB交AC于E.(1)求证:BC=EC;
(2)若BC=4,AC=6,求sin∠D的值.
分析 (1)先由DB=DC,根据等边对等角可得:∠B=∠BCD,然后由$\widehat{AB}$=$\widehat{BC}$,根据等弧所对的圆周角相等可得∠D=∠ACB,然后根据三角形外角的性质可得:∠BEC=∠D+∠DCA,即∠BEC=∠ACB+∠DCA=∠BCD=∠B,然后根据等角对等边,即可得:BC=EC;
(2)连接AB,作BF⊥AC,垂足为F,由$\widehat{AB}$=$\widehat{BC}$,根据等弧所对的弦相等,可得AB=BC=4,然后根据等腰三角形的三线合一可得:AF=CF=$\frac{1}{2}$AC=3,然后由勾股定理可求:BF的值,然后由等弧所对的圆周角相等可得:∠D=∠ACB,进而可得sin∠D=sin∠ACB=$\frac{BF}{BC}$=$\frac{\sqrt{7}}{4}$.
解答 (1)证明:∵DB=DC,
∴∠B=∠BCD,
∵$\widehat{AB}$=$\widehat{BC}$,
∴∠D=∠ACB,
∵∠BEC=∠D+∠DCA,
即∠BEC=∠ACB+∠DCA=∠BCD=∠B,
∴BC=EC;
(2)解:连接AB,作BF⊥AC,垂足为F,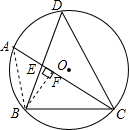
∵$\widehat{AB}$=$\widehat{BC}$,BC=4,
∴AB=BC=4,
∴AF=CF=$\frac{1}{2}$AC=3,
在Rt△BFC中,由勾股定理得:BF=$\sqrt{B{C}^{2}-C{F}^{2}}$=$\sqrt{7}$,
∵∠D=∠ACB,
∴sin∠D=sin∠ACB=$\frac{BF}{BC}$=$\frac{\sqrt{7}}{4}$.
点评 此题考查了圆周角定理,圆周角、弦、弧的关系,等腰三角形的性质及锐角三角函数的定义,解(2)的关键是:添加适当的辅助线,体现转化的思想.

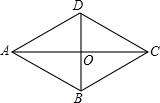 如图,已知菱形ABCD中,对角线AC、BD相交于点O,若AC=8,BD=6,则AB=5.
如图,已知菱形ABCD中,对角线AC、BD相交于点O,若AC=8,BD=6,则AB=5.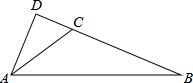 如图,在△ABC中,∠ACB=120°,AC=4,BC=6,过点A作BC的垂线,交BC的延长线于点D,则tanB的值为$\frac{\sqrt{3}}{4}$.
如图,在△ABC中,∠ACB=120°,AC=4,BC=6,过点A作BC的垂线,交BC的延长线于点D,则tanB的值为$\frac{\sqrt{3}}{4}$. 如图,点P在平行四边形ABCD内,且∠ABP=∠ADP,求证:∠DAP=∠DCP.
如图,点P在平行四边形ABCD内,且∠ABP=∠ADP,求证:∠DAP=∠DCP. 在等腰三角形中,过其中的一个顶点的直线如果能把这个等腰三角形分成两个小的等腰三角形,我们称这种等腰三角形为“少见的三角形”,这条直线称为分割线,下面我们来研究这类三角形.
在等腰三角形中,过其中的一个顶点的直线如果能把这个等腰三角形分成两个小的等腰三角形,我们称这种等腰三角形为“少见的三角形”,这条直线称为分割线,下面我们来研究这类三角形. 在平行四边形ABCD中,BE⊥AD于点E,BF⊥CD于点F,若∠EBF=60°,且AE=2,DF=1,则EC的长为4$\sqrt{3}$.
在平行四边形ABCD中,BE⊥AD于点E,BF⊥CD于点F,若∠EBF=60°,且AE=2,DF=1,则EC的长为4$\sqrt{3}$.