题目内容
有A,B两只不透明口袋,每只口袋里装有两只相同的球,A袋中的两只球上分别写了“细”、“心”的字样,B袋中的两只球上分别写了“信”、“任”的字样,从每只口袋里各摸出一只球,能组成“信心”字样的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:列表法与树状图法
专题:
分析:列表得出所有等可能的情况数,找出刚好能组成“信心”字样的情况数,即可求出所求的概率.
解答:解:列表如下:
所有等可能的情况有4种,其中刚好能组成“信心”字样的情况有1种,
则P(能组成“信心”字样)=
.
故选D.
| 细 | 心 | |
| 信 | (细,信) | (心,信) |
| 任 | (细,任) | (心,任) |
则P(能组成“信心”字样)=
| 1 |
| 4 |
故选D.
点评:此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
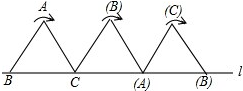 将边长为1cm的等边三角形ABC沿直线l向右翻动(不滑动),点B从开始到结束,所经过路径的长度为( )
将边长为1cm的等边三角形ABC沿直线l向右翻动(不滑动),点B从开始到结束,所经过路径的长度为( )A、
| ||
B、(2+
| ||
| C、πcm | ||
D、2
|
 如图:OB平分∠AOC.且∠2:∠3:∠4=3:5:4,则∠2=
如图:OB平分∠AOC.且∠2:∠3:∠4=3:5:4,则∠2=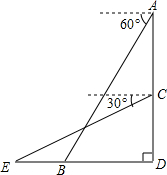 小明在大楼顶部A处测得小亮所在地B处的俯角为60°,当小明下午到大楼的C处时,发现小亮在俯角为30°的E处,E在直线BD上,已知BE=10米,AC=30米,问大楼高多少米?(结果精确到0.1米,
小明在大楼顶部A处测得小亮所在地B处的俯角为60°,当小明下午到大楼的C处时,发现小亮在俯角为30°的E处,E在直线BD上,已知BE=10米,AC=30米,问大楼高多少米?(结果精确到0.1米,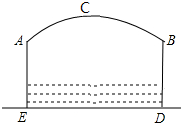 如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE,ED,DB组成,已知河底ED是水平的,ED=16m,AE=8m,抛物线的顶点C到ED的距离是11m.试以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系,求题中抛物线的函数表达式.
如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE,ED,DB组成,已知河底ED是水平的,ED=16m,AE=8m,抛物线的顶点C到ED的距离是11m.试以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系,求题中抛物线的函数表达式.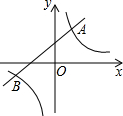 如图,直线y=kx+b与双曲线y=
如图,直线y=kx+b与双曲线y=