题目内容
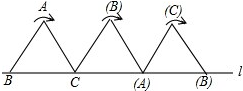将边长为1cm的等边三角形ABC沿直线l向右翻动（不滑动），点B从开始到结束，所经过路径的长度为（ ）A、
| ||
B、（2+
| ||
| C、πcm | ||
D、2
|
考点：弧长的计算,旋转的性质
专题：计算题
分析：点B从开始到结束，所经过路径为两段弧，第一段是以C点为圆心，1cm为半径，圆心角为120°的弧，第二段是以（A）点为圆心，1cm为半径，圆心角为120°的弧，然后根据弧长公式计算．
解答：解：∵△ABC为等边三角形，
∴∠BCA=60°，
∴△ABC每次旋转的度数为120°，
点B从开始到结束，所经过路径的长度=
+
=
π（cm）．
故选A．
∴∠BCA=60°，
∴△ABC每次旋转的度数为120°，
点B从开始到结束，所经过路径的长度=
| 120•π•1 |
| 180 |
| 120•π•1 |
| 180 |
| 4 |
| 3 |
故选A．
点评：本题考查了弧长公式：l=
（弧长为l，圆心角度数为n，圆的半径为R）．也考查了旋转的性质．
| nπR |
| 180 |
练习册系列答案
阅读快车系列答案
相关题目
如图，一个几何体是由一些大小相同的小正方体摆成的，其主视图与左视图如图所示，则组成这个几何体的小正方形最少有已知汽车油箱内有油30L，每行驶100km耗油10L，则汽车行驶过程中油箱内剩余的油量Q（L）与行驶路程s（km）之间的函数表达式是（ ）
A、Q=30-
| ||
B、Q=30+
| ||
C、Q=30-
| ||
D、Q=30+
|
有A，B两只不透明口袋，每只口袋里装有两只相同的球，A袋中的两只球上分别写了“细”、“心”的字样，B袋中的两只球上分别写了“信”、“任”的字样，从每只口袋里各摸出一只球，能组成“信心”字样的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
如图所示，△ABC为⊙O的内接三角形，AB=1，∠C=30°，则⊙O的内接六边形的面积为（ ）A、
| ||||
B、6
| ||||
| C、8 | ||||
| D、16 |
等腰三角形的两边长分别为3cm和7cm，则周长为（ ）cm．
| A、13 | B、17 |
| C、13或17 | D、17或11 |
已知三角形的三边分别为4，a，8，那么该三角形的周长c的取值范围是（ ）
| A、4＜c＜12 |
| B、12＜c＜24 |
| C、8＜c＜24 |
| D、16＜c＜24 |