题目内容
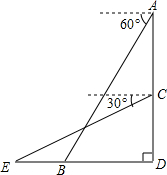 小明在大楼顶部A处测得小亮所在地B处的俯角为60°,当小明下午到大楼的C处时,发现小亮在俯角为30°的E处,E在直线BD上,已知BE=10米,AC=30米,问大楼高多少米?(结果精确到0.1米,
小明在大楼顶部A处测得小亮所在地B处的俯角为60°,当小明下午到大楼的C处时,发现小亮在俯角为30°的E处,E在直线BD上,已知BE=10米,AC=30米,问大楼高多少米?(结果精确到0.1米,| 3 |
考点:解直角三角形的应用-仰角俯角问题
专题:
分析:设AD=x米,则CD=(x-30)米,通过解Rt△ADB得到DE的长度为10+
x;然后解Rt△CDE得到CD=
+
x.结合CD=x=30列出关于x的方程x-30=
+
x,通过解该方程即可得到x即AD的长度.
| ||
| 3 |
10
| ||
| 3 |
| 1 |
| 3 |
10
| ||
| 3 |
| 1 |
| 3 |
解答:解:设AD=x米,则CD=(x-30)米,
在Rt△ADB中,∠BAD=90°-60°=30°,
BD=x•tan30°=
x,DE=BE+BD=10+
x.
在Rt△CDE中,CD=DE•tan30°=(10+
x)•
=
+
x.
又∵CD=x-30,
∴x-30=
+
x.
解得:x=45+5
≈53.7(米),
即楼高为53.7米.
在Rt△ADB中,∠BAD=90°-60°=30°,
BD=x•tan30°=
| ||
| 3 |
| ||
| 3 |
在Rt△CDE中,CD=DE•tan30°=(10+
| ||
| 3 |
| ||
| 3 |
10
| ||
| 3 |
| 1 |
| 3 |
又∵CD=x-30,
∴x-30=
10
| ||
| 3 |
| 1 |
| 3 |
解得:x=45+5
| 3 |
即楼高为53.7米.
点评:本题考查了解直角三角形的应用,解答本题的关键是根据仰角和俯角构造直角三角形,利用三角函数的知识求解,难度一般.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
若圆的半径是5,圆心的坐标是(0,0),点P的坐标是(-4,3),则点P与⊙O的位置关系是( )
| A、点P在⊙O外 |
| B、点P在⊙O内 |
| C、点P在⊙O上 |
| D、点P在⊙O外或⊙O上 |
已知汽车油箱内有油30L,每行驶100km耗油10L,则汽车行驶过程中油箱内剩余的油量Q(L)与行驶路程s(km)之间的函数表达式是( )
A、Q=30-
| ||
B、Q=30+
| ||
C、Q=30-
| ||
D、Q=30+
|
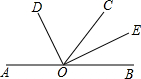 如图,已知A、O、B三点在同一条直线上,OD平分∠AOC,OE平分∠BOC.
如图,已知A、O、B三点在同一条直线上,OD平分∠AOC,OE平分∠BOC.