题目内容
 如图:OB平分∠AOC.且∠2:∠3:∠4=3:5:4,则∠2=
如图:OB平分∠AOC.且∠2:∠3:∠4=3:5:4,则∠2=考点:角平分线的定义
专题:
分析:设∠2=3x,∠3=5x,∠4=4x,根据OB平分∠AOC,故∠1=∠2,然后即可解答.
解答:解:设∠2=3x,∠3=5x,∠4=4x,
根据OB平分∠AOC,故∠1=∠2=3x,
∴∠1+∠2+∠3+∠4=3x+3x+5x+4x=15x=360°,
解得:x=24°,
∴∠2=3x=72°,∠3=5x=120°.
故答案是:72,120.
根据OB平分∠AOC,故∠1=∠2=3x,
∴∠1+∠2+∠3+∠4=3x+3x+5x+4x=15x=360°,
解得:x=24°,
∴∠2=3x=72°,∠3=5x=120°.
故答案是:72,120.
点评:本题考查了角的计算,属于基础题,关键是根据题意列出等式进行求解.

练习册系列答案
相关题目
若圆的半径是5,圆心的坐标是(0,0),点P的坐标是(-4,3),则点P与⊙O的位置关系是( )
| A、点P在⊙O外 |
| B、点P在⊙O内 |
| C、点P在⊙O上 |
| D、点P在⊙O外或⊙O上 |
 如图,把一张长方形纸沿对角线AC折叠后,顶点B落在B′处,已知∠ACB′=28°,那么,∠DCB′=( )
如图,把一张长方形纸沿对角线AC折叠后,顶点B落在B′处,已知∠ACB′=28°,那么,∠DCB′=( )| A、28° | B、31° |
| C、32° | D、34° |
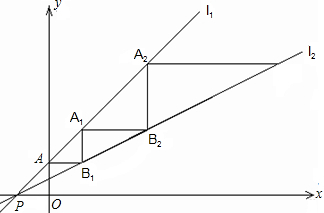 如图,直线l1:y=x+1与直线l2:y=
如图,直线l1:y=x+1与直线l2:y= 如图,一个几何体是由一些大小相同的小正方体摆成的,其主视图与左视图如图所示,则组成这个几何体的小正方形最少有
如图,一个几何体是由一些大小相同的小正方体摆成的,其主视图与左视图如图所示,则组成这个几何体的小正方形最少有 小李和小陆从A地出发,骑自行车沿同一条路行驶到B地.小陆因为有事,在A地停留0.5小时后出发,1小时后他们相遇,两人约定,谁先到B地就在原地等待.他们离出发地的距离S(单位:km)和行驶时间t(单位:h)之间的函数关系的图象如图所示.
小李和小陆从A地出发,骑自行车沿同一条路行驶到B地.小陆因为有事,在A地停留0.5小时后出发,1小时后他们相遇,两人约定,谁先到B地就在原地等待.他们离出发地的距离S(单位:km)和行驶时间t(单位:h)之间的函数关系的图象如图所示.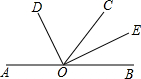 如图,已知A、O、B三点在同一条直线上,OD平分∠AOC,OE平分∠BOC.
如图,已知A、O、B三点在同一条直线上,OD平分∠AOC,OE平分∠BOC.