题目内容
4.分解因式:(1)m2+m;
(2)x2+4xy+4y2;
(3)3m2n-12mn+12n.
分析 (1)根据提公因式法,可得答案;
(2)根据完全平方公式,可得答案;
(3)根据提公因式,可得完全平方公式,根据完全平方公式,可得答案.
解答 解:(1)m2+m=m(m+1);
(2)x2+4xy+4y2=(x+2y)2;
(3)3m2n-12mn+12n=3n(m2-4m+4)=3n(m-2)2.
点评 本题考查了因式分解,提取公因式后利用完全平方公式进行二次分解,注意分解要彻底.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
15. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的有( )
①ac>0.②当x>1时,y随x的增大而减小.③b-2a=0.④b2-4ac>0.⑤x=3是关于x的方程ax2+bx+c=0(a≠0)的一个根.
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的有( )①ac>0.②当x>1时,y随x的增大而减小.③b-2a=0.④b2-4ac>0.⑤x=3是关于x的方程ax2+bx+c=0(a≠0)的一个根.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.用配方法解方程x2+4x-3=0,配方后的方程可以是( )
| A. | (x-2)2=1 | B. | (x+2)2=1 | C. | (x-2)2=7 | D. | (x+2)2=7 |
16. y=kx+b的图象如图,当y<0时,自变量x的范围是( )
y=kx+b的图象如图,当y<0时,自变量x的范围是( )
 y=kx+b的图象如图,当y<0时,自变量x的范围是( )
y=kx+b的图象如图,当y<0时,自变量x的范围是( )| A. | x<-2 | B. | x>0 | C. | x<0 | D. | x>2 |
14.下列各式没有意义的是( )
| A. | $\sqrt{3^2}$ | B. | $\sqrt{-{3^2}}$ | C. | $\sqrt{{{({-3})}^2}}$ | D. | ${({\sqrt{3}})^2}$ |
 小张想测量某建筑物AB的高度,在C处测得建筑物顶部A的仰角为30°,然后沿CB前进100米到达D处,测得顶部A的仰角为60°,求建筑物AB的高度.(结果保留根号)
小张想测量某建筑物AB的高度,在C处测得建筑物顶部A的仰角为30°,然后沿CB前进100米到达D处,测得顶部A的仰角为60°,求建筑物AB的高度.(结果保留根号)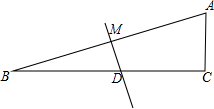 如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交BC于点D,交AB于点M,BD=8cm,求AC的长.
如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交BC于点D,交AB于点M,BD=8cm,求AC的长.