题目内容
14．
如图所示，以平行四边形ABCD的顶点A为圆心，AB为半径作圆，作AD，BC于E，F，延长BA交⊙A于G，判断弧EF和EG是否相等，并说明理由．
分析 要证明$\widehat{\widehat{EF}}$=$\widehat{GE}$，则要证明∠DAF=∠GAD，由AB=AF，得出∠ABF=∠AFB，平行四边形的性质得出，AFB=∠DAF，∠GAD=∠ABF，由圆心角、弧、弦的关系定理得出$\widehat{\widehat{EF}}$=$\widehat{GE}$．
解答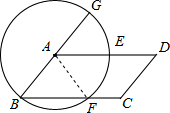 
解：相等．
理由：连接AF．
∵A为圆心，
∴AB=AF，
∴∠ABF=∠AFB，
∵四边形ABCD为平行四边形，
∴AD∥BC，∠AFB=∠DAF，∠GAD=∠ABF，
∴∠DAF=∠GAD，
∴$\widehat{\widehat{EF}}$=$\widehat{GE}$．
点评 本题考查了平行四边形性质，平行线性质，圆心角、弧、弦的关系定理等知识点的应用，关键是求出∠DAF=∠GAD，题目比较典型，难度不大．
练习册系列答案
相关题目
利用数轴解下列各题：
19．在①4a5b3c2÷（-2a2bc）=abc；②（3.6×10-4）÷4×10-5=9；③$4{x^2}y•（-\frac{1}{2}y）÷4{x^2}{y^2}=-\frac{1}{2}$；④（4xn）2÷xn=8x2n-2中，不正确的个数是（ ）
| A． | 0个 | B． | 1个 | C． | 2个 | D． | 3个 |
6．若分式$\frac{|m|-1}{{{m^2}-m}}$的值为零，则m取值为（ ）
| A． | m=±1 | B． | m=-1 | C． | m=1 | D． | m的值不存在 |