题目内容
19. 如图,E是AB上一点,F是DC上一点,G是BC延长线上一点,下列能判断AB∥CD的是( )
如图,E是AB上一点,F是DC上一点,G是BC延长线上一点,下列能判断AB∥CD的是( )| A. | ∠A+∠B=180° | B. | ∠D=∠DCG | C. | ∠B=∠DCG | D. | ∠B=∠AEF |
分析 由平行线的判定方法得出C选项能判断AB∥CD,A、B、D不能判断AB∥CD,即可得出结论.
解答 解:∵∠A+∠B=180°,
∴AD∥BC,不能得出AB∥CD,
∴A不能;
∵∠D=∠DCG,
∴AD∥BC,不能得出AB∥CD,
∴B不能;
∵∠B=∠DCG,
∴AB∥CD,
∴C能;
∵∠B=∠AEF,
∴AD∥EF,不能得出AB∥CD,
∴D不能;
故选:C.
点评 本题考查了平行线的判定方法;熟练掌握平行线的判定方法是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.若-4a5b2m与3a2m+3bn+3的和仍一个是单项式,则m、n的值分别是( )
| A. | 1,-1 | B. | 1,2 | C. | 1,-2 | D. | 1,1 |
14.下列各式没有意义的是( )
| A. | $\sqrt{3^2}$ | B. | $\sqrt{-{3^2}}$ | C. | $\sqrt{{{({-3})}^2}}$ | D. | ${({\sqrt{3}})^2}$ |
11.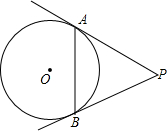 如图,PA、PB是圆O的切线,切点分别是A、B,如果∠P=60°,那么弦AB所对的圆周角等于( )
如图,PA、PB是圆O的切线,切点分别是A、B,如果∠P=60°,那么弦AB所对的圆周角等于( )
 如图,PA、PB是圆O的切线,切点分别是A、B,如果∠P=60°,那么弦AB所对的圆周角等于( )
如图,PA、PB是圆O的切线,切点分别是A、B,如果∠P=60°,那么弦AB所对的圆周角等于( )| A. | 60° | B. | 120° | C. | 30°或120° | D. | 60°或120° |
8.下列关于x的方程中,一定是一元二次方程的为( )
| A. | 2x+3=0 | B. | x2-2=(x+3)2 | C. | ${x^2}=\frac{1}{x}$ | D. | x2-1=0 |
9.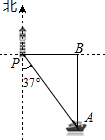 如图,一艘海轮位于灯塔P的南偏东37°方向,距离灯塔40 海里的A处,它沿正北方向航行一段时间后,到达位于灯塔P的正东方向上的B处.这时,B处与灯塔P的距离BP的长可以表示为( )
如图,一艘海轮位于灯塔P的南偏东37°方向,距离灯塔40 海里的A处,它沿正北方向航行一段时间后,到达位于灯塔P的正东方向上的B处.这时,B处与灯塔P的距离BP的长可以表示为( )
 如图,一艘海轮位于灯塔P的南偏东37°方向,距离灯塔40 海里的A处,它沿正北方向航行一段时间后,到达位于灯塔P的正东方向上的B处.这时,B处与灯塔P的距离BP的长可以表示为( )
如图,一艘海轮位于灯塔P的南偏东37°方向,距离灯塔40 海里的A处,它沿正北方向航行一段时间后,到达位于灯塔P的正东方向上的B处.这时,B处与灯塔P的距离BP的长可以表示为( )| A. | 40海里 | B. | 40tan37°海里 | C. | 40cos37°海里 | D. | 40sin37°海里 |