题目内容
7.已知关于x的方程(m2-m)x2-2mx+1=0(i)与x2+2$\sqrt{3}$x+m=0(ii)都有两个不相等的实数根,且m为整数.若a是方程(m2-m)x2-2mx+1=0的一个根,求代数式:①$\frac{1}{2}$a2-a+1=0;②2a2-3a-$\frac{2{a}^{2}+1}{4}$+3;③2a2-2a+$\frac{2a}{4a-1}$的值.分析 先由关于x的方程(m2-m)x2-2mx+1=0(i)与x2+2$\sqrt{3}$x+m=0(ii)都有两个不相等的实数根,根据一元二次方程的定义及根的判别式的意义求出m的取值范围是0<m<3,且m≠1,又由m为整数,得到m=2,再根据一元二次方程的解的定义,将x=a代入方程,得出2a2-4a+1=0,则2a2-4a=-1,2a2=4a-1,2a2+1=4a.分别代入所求代数式,即可求解.
解答 解:∵关于x的方程(m2-m)x2-2mx+1=0有两个不相等的实数根,
∴m2-m≠0,且△=(-2m)2-4(m2-m)>0,
解得,m>0,且m≠1;
∵关于x的方程x2+2$\sqrt{3}$x+m=0有两个不相等的实数根,
∴△=(2$\sqrt{3}$)2-4m>0,
解得,m<3,
∴0<m<3,且m≠1,
又∵m为整数,
∴m=2,
∴方程(i)即为2x2-4x+1=0.
∵a是方程2x2-4x+1=0的一个根,
∴2a2-4a+1=0,
∴2a2-4a=-1,2a2=4a-1,2a2+1=4a.
①$\frac{1}{2}$a2-a+1=$\frac{1}{4}$(2a2-4a)+1=$\frac{1}{4}$×(-1)+1=$\frac{3}{4}$;
②2a2-3a-$\frac{2{a}^{2}+1}{4}$+3=4a-1-3a-$\frac{4a}{4}$+3=2;
③2a2-2a+$\frac{2a}{4a-1}$=4a-1-2a+$\frac{2a}{2{a}^{2}}$=2a-1+$\frac{1}{a}$=$\frac{2{a}^{2}-a+1}{a}$=$\frac{4a-1-a+1}{a}$=3.
点评 本题主要考查了一元二次方程的解的定义与根的判别式.解答此题的关键是求出m=2.

| A. | $\frac{-x-y}{-x+y}$=$\frac{x-y}{x+y}$ | B. | $\frac{y-x}{(x-y)^{2}}$=$\frac{1}{x-y}$ | ||
| C. | $\frac{{x}^{2}-{y}^{2}}{(y-x)^{2}}$=$\frac{x+y}{x-y}$ | D. | $\frac{y-x}{{x}^{2}-{y}^{2}}$=$\frac{1}{x+y}$ |
| A. | 5 | B. | -2.25 | C. | 0 | D. | 8.3 |
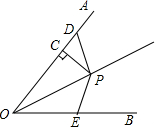 如图,P为∠AOB的平分线上的一点,PC⊥OA于点C,D为OA上一点,E为OB上一点,∠ODP+∠OEP=180°,当OC=6.5cm时,OD+OE=13cm.
如图,P为∠AOB的平分线上的一点,PC⊥OA于点C,D为OA上一点,E为OB上一点,∠ODP+∠OEP=180°,当OC=6.5cm时,OD+OE=13cm.