题目内容
18.下列运算正确的是( )| A. | $\frac{-x-y}{-x+y}$=$\frac{x-y}{x+y}$ | B. | $\frac{y-x}{(x-y)^{2}}$=$\frac{1}{x-y}$ | ||
| C. | $\frac{{x}^{2}-{y}^{2}}{(y-x)^{2}}$=$\frac{x+y}{x-y}$ | D. | $\frac{y-x}{{x}^{2}-{y}^{2}}$=$\frac{1}{x+y}$ |
分析 根据分式的基本性质进行解答即可.
解答 解:A、原式=$\frac{x+y}{x-y}$,故本选项错误;
B、原式=-$\frac{1}{x-y}$,故本选项错误;
C、原式=$\frac{(x+y)(x-y)}{(x-y)^{2}}$=$\frac{x+y}{x-y}$,故本选项正确;
D、原式=$\frac{x-y}{(y+x)(y-x)}$=-$\frac{1}{x+y}$,故本选项错误;
故选:C.
点评 本题考查了分式的基本性质.解题的关键是正确运用分式的基本性质.
规律总结:(1)同类分式中的操作可总结成口诀:“一排二添三变”,
“一排”即按同一个字母的降幂排列;
“二添”是把第一项系数为负号的分子或分母添上带负号的括号;
“三变”是按分式变号法则把分子与分母的负号提到分式本身的前边.
(2)分式的分子、分母及本身的符号,任意改变其中的两个,分式的值不变.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
8.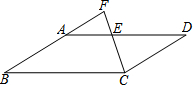 如图,在平行四边形ABCD中,点E在AD边上,连接CE并延长,交BA的延长线于点F.若AE=$\frac{5}{13}$AD,CD=3,则AF的长为( )
如图,在平行四边形ABCD中,点E在AD边上,连接CE并延长,交BA的延长线于点F.若AE=$\frac{5}{13}$AD,CD=3,则AF的长为( )
 如图,在平行四边形ABCD中,点E在AD边上,连接CE并延长,交BA的延长线于点F.若AE=$\frac{5}{13}$AD,CD=3,则AF的长为( )
如图,在平行四边形ABCD中,点E在AD边上,连接CE并延长,交BA的延长线于点F.若AE=$\frac{5}{13}$AD,CD=3,则AF的长为( )| A. | $\frac{15}{13}$ | B. | $\frac{24}{13}$ | C. | $\frac{24}{5}$ | D. | $\frac{15}{8}$ |