题目内容
17．先化简，再求值：（$\frac{x+2}{x}$-$\frac{x-1}{x-2}$）÷$\frac{x-4}{{x}^{2}-4x+4}$，其中x=3．分析 先根据分式混合运算的法则把原式进行化简，再求出x的值代入进行计算即可．
解答 解：原式=$\frac{{x}^{2}-4-{x}^{2}+x}{x（x-2）}$•$\frac{（x-2）^{2}}{x-4}$
=$\frac{x-4}{x（x-2）}$•$\frac{{（x-2）}^{2}}{x-4}$
=$\frac{x-2}{x}$，
当x=3时，原式=$\frac{1}{3}$．
点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
练习册系列答案
相关题目
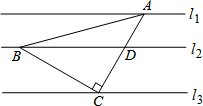如图，直线l1∥l2∥l3，且l1与l3之间的距离为$\sqrt{3}$，l2与l3之间的距离为1．若点A，B，C分别在直线l1，l2，l3上，且AC⊥BC，AC=BC，AC与直线l2交于点D，则BD的长为$\frac{4\sqrt{3}}{3}$．
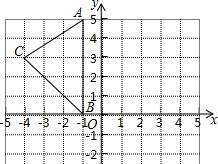如图，在平面直角坐标系xOy中，A（-1，5），B（-1，0），C（-4，3），在图中作出△ABC关于y轴的对称图形△A1B1C1，并写出A1点关于x轴对称的点的坐标．