题目内容
19.阅读材料:为解方程(x2-1)2-5(x2-1)+4=0,我们可以将x2-1看作一个整体,然后设x2-1=y,那么原方程可化为y2-5y+4=0①,解得y1=1,y2=4.当y=1时,x2-1=1,∴x=±$\sqrt{2}$;当y=4时,x2-1=4,∴x2=5,∴x=±$\sqrt{5}$,故原方程的解为x1=$\sqrt{2}$,x2=-$\sqrt{2}$,x3=$\sqrt{5}$,x4=-$\sqrt{5}$.解答问题:
(1)上述解题过程,在由原方程得到方程①的过程中,利用换元法达到了解方程的目的,体现了转化的数学思想;
(2)请利用以上知识解决:若(m2+n2-2)(m2+n2)=8,求m2+n2的值.
分析 (1)根据题目的变形可以看出运用了换元法和整体思想在解答这道题,故得出结论为换元法.
(2)先设m2+n2=y,原方程可以变为:(y-2)y=8,再解一道关于y的方程求出y的值,即m2+n2的值.
解答 解:(1)∵将x2-1看作一个整体,然后设x2-1=y,实际上是将x2-1转化为了y,
∴这一步是运用了数学里的转化思想,这种方法交换元法.
故答案为:换元.
(2)设m2+n2=y,则原方程变形为:(y-2)y=8,
整理,得(y-4)(y+2)=0,
解得y=4或y=-2(舍去),
即m2+n2=4.
点评 本题主要考查了换元法,即把某个式子看作一个整体,用一个字母去代替它,实行等量替换.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
4.下列各式正确的是( )
| A. | 2a+3b=5ab | B. | a+2a=3a2 | C. | 2a2-a2=2 | D. | b2-2b2=-b2 |
8.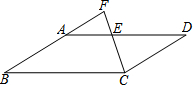 如图,在平行四边形ABCD中,点E在AD边上,连接CE并延长,交BA的延长线于点F.若AE=$\frac{5}{13}$AD,CD=3,则AF的长为( )
如图,在平行四边形ABCD中,点E在AD边上,连接CE并延长,交BA的延长线于点F.若AE=$\frac{5}{13}$AD,CD=3,则AF的长为( )
 如图,在平行四边形ABCD中,点E在AD边上,连接CE并延长,交BA的延长线于点F.若AE=$\frac{5}{13}$AD,CD=3,则AF的长为( )
如图,在平行四边形ABCD中,点E在AD边上,连接CE并延长,交BA的延长线于点F.若AE=$\frac{5}{13}$AD,CD=3,则AF的长为( )| A. | $\frac{15}{13}$ | B. | $\frac{24}{13}$ | C. | $\frac{24}{5}$ | D. | $\frac{15}{8}$ |
9.下列交通标志既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |