题目内容
17.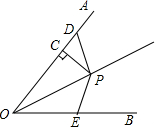 如图,P为∠AOB的平分线上的一点,PC⊥OA于点C,D为OA上一点,E为OB上一点,∠ODP+∠OEP=180°,当OC=6.5cm时,OD+OE=13cm.
如图,P为∠AOB的平分线上的一点,PC⊥OA于点C,D为OA上一点,E为OB上一点,∠ODP+∠OEP=180°,当OC=6.5cm时,OD+OE=13cm.
分析 作PF⊥OB于F,根据角平分线的性质就可以得出PC=PF,根据HL可以判断Rt△PCO≌Rt△PFO,从而可得OC=OF,然后根据AAS就可以得出△CDP≌△EFP,从而得到CD=EF,进而得出DO+E0=13cm.
解答 证明:过P作PF⊥OB于F,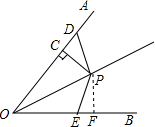 ∴∠PFO=90°,
∴∠PFO=90°,
∵P为∠AOB的平分线OP上一点,PC⊥OA,
∴PC=PF,∠PCA=90°,
∴∠PCA=∠PFO,
在Rt△PCO和RtPFO中,
$\left\{\begin{array}{l}{PO=PO}\\{PC=PF}\end{array}\right.$,
∴Rt△PCO≌Rt△PFO(HL),
∴OC=OF.
∵∠ODP+∠OEP=180°,且∠OEP+∠PEB=180°,
∴∠ODP=∠FEP,
在△CDP和△EFP中,
$\left\{\begin{array}{l}{∠PCD=∠PFE}\\{∠CDP=∠PEF}\\{PC=PF}\end{array}\right.$,
∴△CDP≌△EFP(AAS),
∴CD=EF,
∵DO+EO=DC+CO+EO,
∴DO+EO=EF+EO+CO,
∴DO+EO=FO+CO,
∴DO+EO=2CO,
∵CO=6.5cm,
∴DO+E0=13cm.
故答案为:13cm.
点评 本题考查了角平分线的性质的运用,直角三角形的性质的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目
8.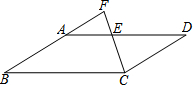 如图,在平行四边形ABCD中,点E在AD边上,连接CE并延长,交BA的延长线于点F.若AE=$\frac{5}{13}$AD,CD=3,则AF的长为( )
如图,在平行四边形ABCD中,点E在AD边上,连接CE并延长,交BA的延长线于点F.若AE=$\frac{5}{13}$AD,CD=3,则AF的长为( )
 如图,在平行四边形ABCD中,点E在AD边上,连接CE并延长,交BA的延长线于点F.若AE=$\frac{5}{13}$AD,CD=3,则AF的长为( )
如图,在平行四边形ABCD中,点E在AD边上,连接CE并延长,交BA的延长线于点F.若AE=$\frac{5}{13}$AD,CD=3,则AF的长为( )| A. | $\frac{15}{13}$ | B. | $\frac{24}{13}$ | C. | $\frac{24}{5}$ | D. | $\frac{15}{8}$ |
2.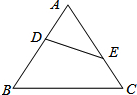 如图,在△ABC中,已知∠AED=∠B,DE=6;AB=10,AE=5,则BC的长为( )
如图,在△ABC中,已知∠AED=∠B,DE=6;AB=10,AE=5,则BC的长为( )
 如图,在△ABC中,已知∠AED=∠B,DE=6;AB=10,AE=5,则BC的长为( )
如图,在△ABC中,已知∠AED=∠B,DE=6;AB=10,AE=5,则BC的长为( )| A. | 3 | B. | 12 | C. | $\frac{25}{3}$ | D. | 7 |
9.下列交通标志既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
6.已知-1是关于x的方程x2+4x-m=0的一个根,则这个方程的另一个根是( )
| A. | -3 | B. | -2 | C. | -1 | D. | 3 |
 如图,△ABC中,∠BAC=60°,D,E两点在直线BC上,连接AD,AE,则∠1+∠2+∠3+∠4=120°.
如图,△ABC中,∠BAC=60°,D,E两点在直线BC上,连接AD,AE,则∠1+∠2+∠3+∠4=120°.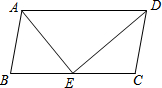 如图,在?ABCD中,DE是∠ADC的平分线,交BC于点E.
如图,在?ABCD中,DE是∠ADC的平分线,交BC于点E.